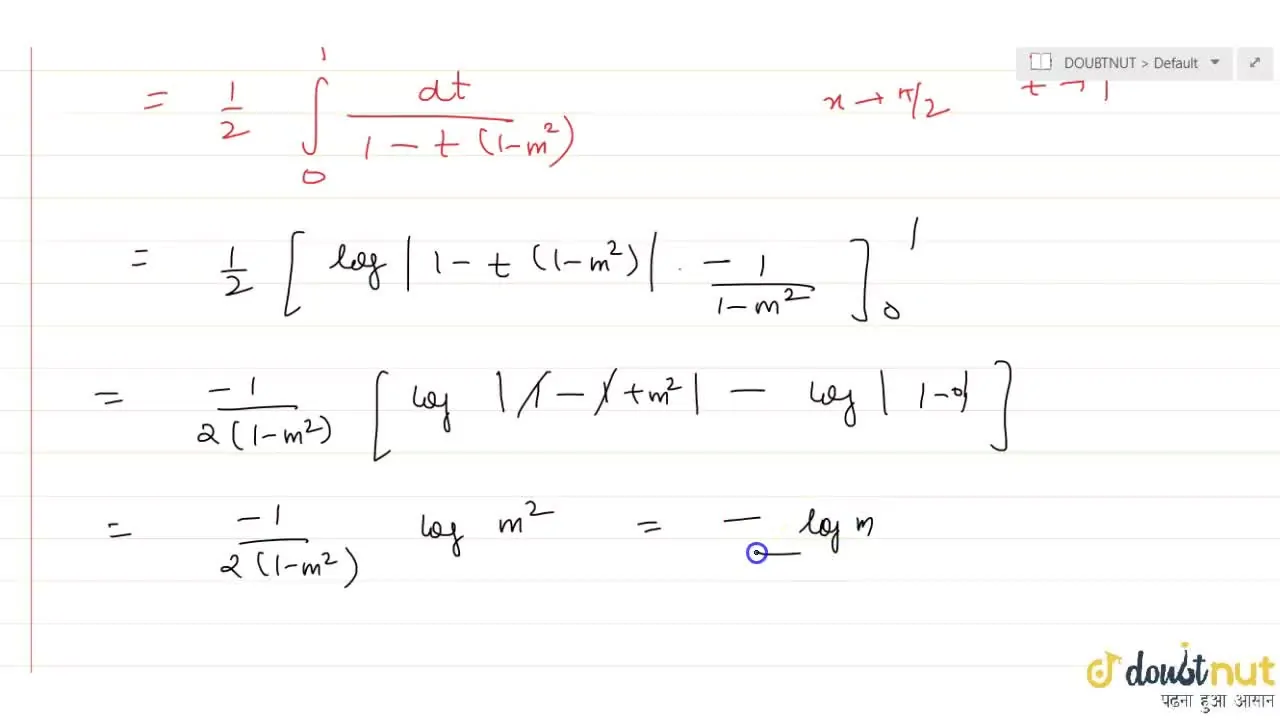∫π/20tanx1+m2tan2x dx
Video Solution
Text Solution
The correct Answer is:N/a
Let I=∫π/20tanxdx1+m2tan2xdx
=∫π/20sinxcosx1+m2.sin2xcos2xdx
=∫π/20sinxcosxcos2x+m2sin2xcos2xdx
=∫π/20sinxcosxdx1−sin2x+m2sin2xdx
=∫π/20sinxcosx1−sin2x(1−m2)dx
Put sin2x=t
⇒2sinxcosxdx=dt
∴I=12∫10dt1−t(1−m2)
=12[−log∣∣1−t(1−m2)∣∣.11−m2]10
=12[−log∣∣1−1+m2∣∣.11+m2+log|1|.11+m2]
=12[−log∣∣m2∣∣.11−m2]=22.logm(m2−1)
log'mm2−1
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Evaluate the following integrals: ∫π/20tanx1+m2tan2xdx
View Solution∫π/20log(tanx)dx
View Solution∫π/20tanx(1+tanx)dx=?
View SolutionThe value of ∫π/20dx1+tan3x is
View SolutionThe value of ∫π/20tanxlog(tanx)sec2xdx is
View Solution∫π/20dx1+tan5x
View SolutionThe value of ∫π/20dx1+tan3x is
View Solution∫π/20xtanxdx=
View Solution∫π/40ex(1+tanx+tan2x)dx=
View SolutionThe value of ∫−π/401+tanx1−tanxdx is
View Solution