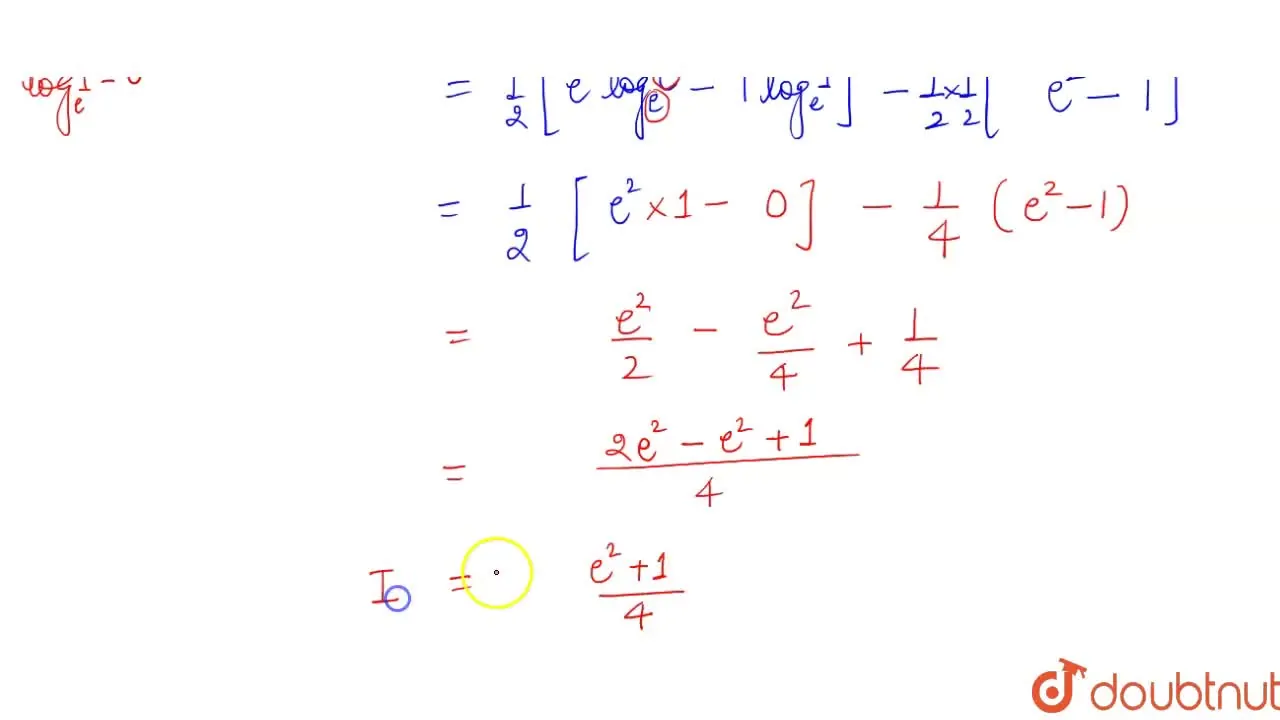∫e1xlnxdx, किसके बराबर है ?
A
e+14
B
e2+14
C
e−14
D
e2−14
Video Solution
Text Solution
The correct Answer is:B
माना l=∫e1xlogxdx
[logx.∫xdx]e1−∫e1[ddx{logx}.∫xdx]d
=[logx.x22]e1−∫e11x.x22dx
=e22−12×12[x2]e1
=e22−[e2−1]4
=2e2−e2+14=e2+14
|
Updated on:21/07/2023
Related Playlists
Similar Questions
यदि x+lgo10(1+2x)=xlog105+log106, तो x किसके बराबर है ?
03:02View Solutionlog7log7√7√7√7 का मान, किसके बराबर है ?
01:31View Solutionint_(e^(-1))^(e^(2))|(ln x)/(x)|dx
01:54View Solutionint_(1)^(e)(dx)/(x(1+log x))
03:57View Solutionint_(1)^(e^(2))(dx)/(x(1+log x)^(2))=
03:38View Solutionint_((1)/(e))^(e)|log x|dx=
01:32View Solutionint_((1)/(e))^(1)|(ln x)/(x)|dx=
02:06View SolutionThe value of int_(1)^(e)(1)/(x)(1+log x)dx is
06:37View Solution∫e1/edxx(logx)1/3
01:49View SolutionThe value of ∫e1/e|logx|x2dx, is
01:05View Solution∫e1logxxdx
03:08View Solution∫log20ex1+exdx=
03:37View Solution∫e1xxdx+∫e1xxlogxdx=
02:33View Solution∫e1log(x)dx=
01:24View Solution∫e11+logxxdx=
03:28View Solution∫e11+logxxdx=
02:54View Solution