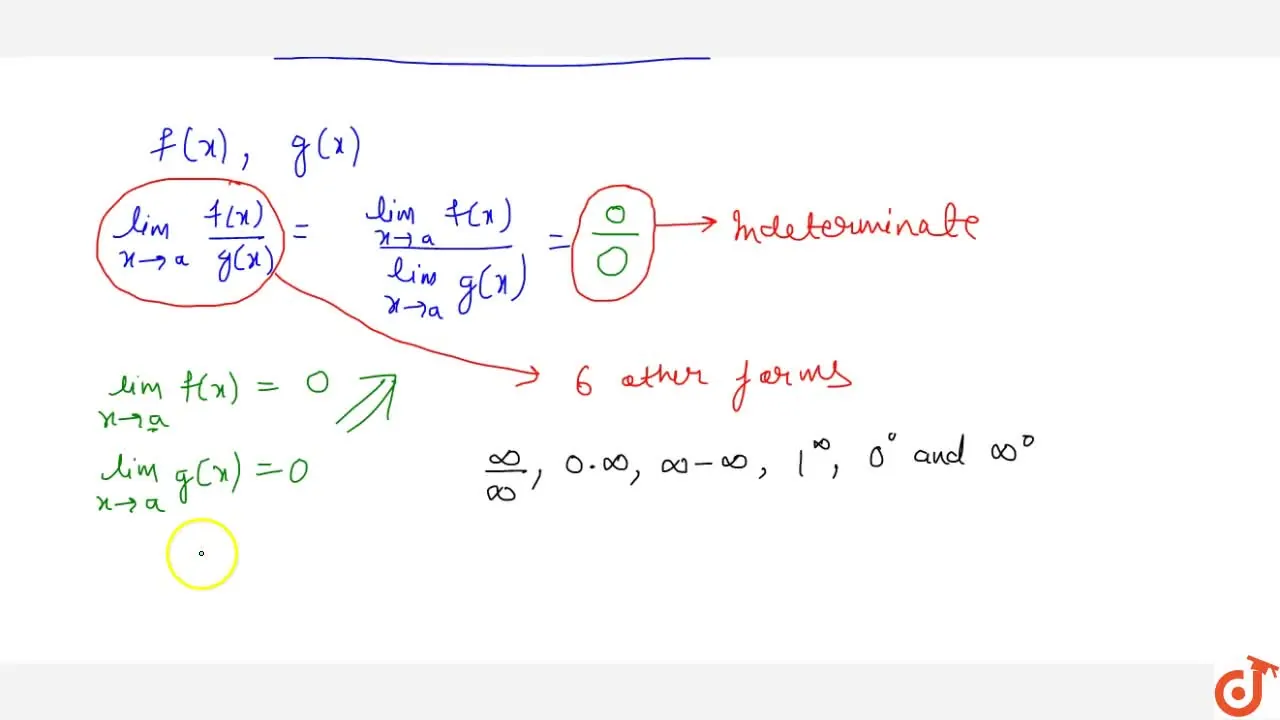
Introduction of all indeterminate forms
Step by step video & image solution for Introduction of all indeterminate forms by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
Indeterminate form 1^(∞)
View SolutionIntroduction OF Solution || Solute and Solvent || Classification OF Solutions- On the Basis OF Components OF Solutions/On the OF Amount OF Solute ||Meaning OF Concentration || Introduction OF all Concentration Terms
View SolutionIndeterminate species
View SolutionWhich of the following limits are in indeterminate forms. Also indicate the form
limx→0(1)1xView SolutionDeuterostome condition and indeterminate radial cleavage are characteristic of
View SolutionDeuterostome condition and indeterminate radial cleavage are characteristics of
View SolutionThere is no definite information about indeterminate species.
View SolutionCheck given limits is in indeterminate forms or not?. Also indicate the form
limx→0(1+sinx)1xView SolutionCheck given limit is in indeterminate form or not? Also indicate the form
limx→01xView SolutionCheck given limits is in indeterminate form or not? Also indicate the form
limx→0(sinx)xView Solution