Inverse variation if two quantities x and y vary with each other in such a manner that the product of remains constant and is positive then we say that a and b vary inversely as each other or a varies inversely as b and b varies inversely as a
Step by step video & image solution for Inverse variation if two quantities x and y vary with each other in such a manner that the product of remains constant and is positive then we say that a and b vary inversely as each other or a varies inversely as b and b varies inversely as a by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIRECT AND INVERSE PROPORTIONS BOOK - NCERT EXEMPLARCHAPTER - DIRECT AND INVERSE PROPORTIONS EXERCISE - THINK AND DISCUSS
2 Videos
- DIRECT AND INVERSE PROPORTIONS BOOK - NCERT EXEMPLARCHAPTER - DIRECT AND INVERSE PROPORTIONS EXERCISE - THINK AND DISCUSS
2 Videos
- DATA HANDLINGBOOK - NCERT EXEMPLARCHAPTER - DATA HANDLINGEXERCISE - EXERCISE
73 Videos
- EXPONENTS AND POWERSBOOK - NCERT EXEMPLARCHAPTER - EXPONENTS AND POWERSEXERCISE - EXERCISE
195 Videos
Similar Questions
Knowledge Check
If two quantities x and y vary inversely with each other, then which one of the following is true?
AProduct of their corresponding values remains constant.BSummation of their corresponding values remains constant.CDifference of their corresponding values remains constant.DRatio of their corresponding values remains constant
If two quantities p and q vary inversely with each other, then
View SolutionIf x varies inversely as y, then
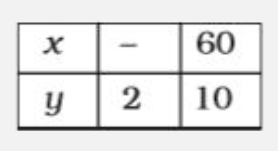
View SolutionIf x varies as yz, then y varies inversely as
View SolutionIf on increasing a, b decreases in such a manner that _______ remains ______constant and positive, then a and b are said to vary inversely with each other.
View SolutionIf x = 5y, then x and y vary ______ with each other
View SolutionIf a and b vary inversely to each other, then find the values of p, q, r .
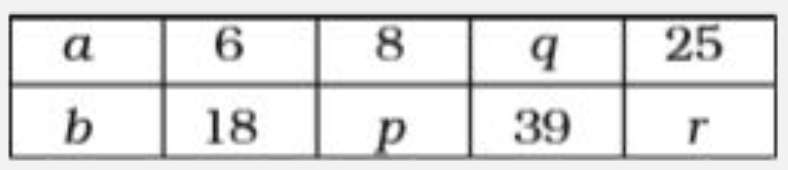
View SolutionIf a and b vary inversely to each other, then find the values of l, m, n.
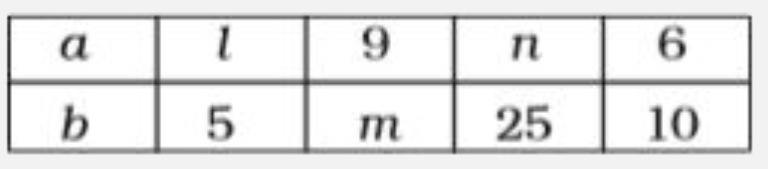
View Solution
