It is given that ∠XYZ=64∘ and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.
To solve the problem step by step, let's break it down:
Step 1: Draw the figure
- Start by drawing a line segment XY.
- At point Y, draw a ray YZ such that the angle ∠XYZ = 64°.
- Extend the line XY to point P, making sure that P lies on the same line as XY.
- Draw a ray YQ that bisects the angle ∠ZYP.
Step 2: Identify the angles
- Let ∠ZYP be divided into two equal angles by ray YQ. Denote these angles as x. Therefore, we have:
- ∠ZYP = 2x
- ∠QYZ = x
Step 3: Use the linear pair of angles
- Since ∠XYZ, ∠ZYP, and ∠QYZ are adjacent angles along the line, we can write the equation:
∠XYZ+∠ZYP+∠QYZ=180°
Substituting the known values:
64°+2x=180°
Step 4: Solve for x
- Rearranging the equation gives:
2x=180°−64°
2x=116°
x=116°2=58°
Step 5: Find ∠XYQ
- Now, we can find ∠XYQ:
∠XYQ=∠XYZ+∠QYZ=64°+58°=122°
Step 6: Find ∠QYP
- We know that ∠QYP = x, which we calculated to be:
∠QYP=58°
Step 7: Find the reflex angle ∠QYP
- The reflex angle ∠QYP is calculated as:
Reflex ∠QYP=360°−∠QYP=360°−58°=302°
Final Answers:
- ∠XYQ = 122°
- Reflex ∠QYP = 302°
- Start by drawing a line segment XY.
- At point Y, draw a ray YZ such that the angle ∠XYZ = 64°.
- Extend the line XY to point P, making sure that P lies on the same line as XY.
- Draw a ray YQ that bisects the angle ∠ZYP.
- Let ∠ZYP be divided into two equal angles by ray YQ. Denote these angles as x. Therefore, we have:
- ∠ZYP = 2x
- ∠QYZ = x
- Since ∠XYZ, ∠ZYP, and ∠QYZ are adjacent angles along the line, we can write the equation:
∠XYZ+∠ZYP+∠QYZ=180°
Substituting the known values:
64°+2x=180°
- Rearranging the equation gives:
2x=180°−64°
2x=116°
x=116°2=58°
- Now, we can find ∠XYQ:
∠XYQ=∠XYZ+∠QYZ=64°+58°=122°
- We know that ∠QYP = x, which we calculated to be:
∠QYP=58°
- The reflex angle ∠QYP is calculated as:
Reflex ∠QYP=360°−∠QYP=360°−58°=302°
- ∠XYQ = 122°
- Reflex ∠QYP = 302°
Topper's Solved these Questions
- LINES AND ANGLESBOOK - NCERT ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - SOLVED EXAMPLES
8 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - NCERT ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Exercise 4.1
2 Videos
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.12
1 Videos
Similar Questions
Knowledge Check
In Figure 1, y=√3xandz=2x. What is the ratio p:q:r in figure 2?
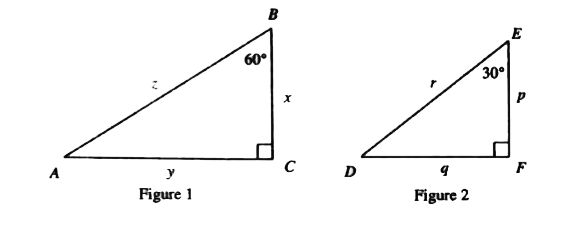 A1:2:3B√3:1:2C1:√3/2:1D2:√3:1
A1:2:3B√3:1:2C1:√3/2:1D2:√3:1
In the figure, P is the centre of the circle. Prove that: ∠XPZ=2 (∠XZY+ ∠YXZ)
View SolutionA is (-2, 0) and P is any point on the curve given by y2=16x. If Q bisect AP, find the equation of the locus of Q.
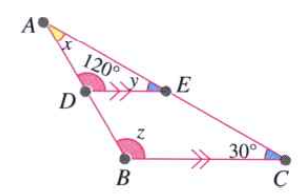
View SolutionFind the values of x,y and z in the given figure.

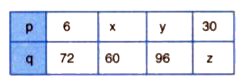
View SolutionIF p and q are in direct variation of x, y and z in the table given below:
View SolutionIn the given figure l||mandp||q. Find the angle x,y, z
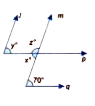
View SolutionIn the given figure, l||mandp||q. Find the angles x, y and z

View SolutionIn Figure, given that △ABC~△PQR and ABCD~ PQRS . Determine the values of x, y, z in each case.
View Solution