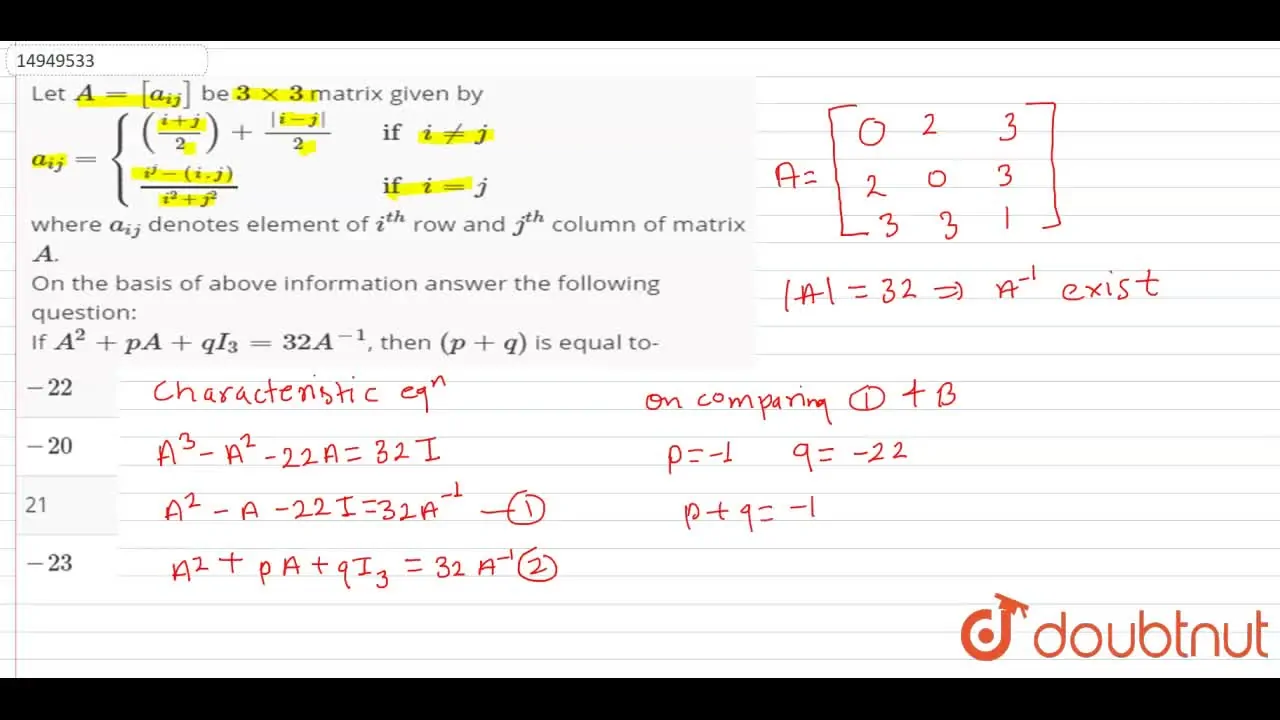
Let A=[aij] be 3×3 matrix given by aij=⎧⎪
⎪⎨⎪
⎪⎩(i+j2)+|i−j|2ifi≠jij−(i.j)i2+j2ifi=j
where aij denotes element of ith row and jth column of matrix A.
On the basis of above information answer the following question:
If A2+pA+qI3=32A−1, then (p+q) is equal to-
−22
−20
21
−23
The correct Answer is:D
We have A=⎡⎢⎣023203331⎤⎥⎦
⇒|A|=32⇒A−1 will exist
Also matrix A is non-singular
∴ The characteristic equation of matrix A, is
⇒A3−A2−22A=32I
⇒32A−1=A2−A−22I
∴p=−1,q=−22 (on comparing)
⇒(p+q)=−23
Also, A2−A=B2−B2 (Given)
⇒|A||A−I|=|B|2|A−I|
As |A−I|≠0
⇒|B|2=|A|=32
∴∣∣√2BA−1∣∣=2√2|B||A|
2√2(±4√2)32=±1632=±12
Related Playlists
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 Mathematics18videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 Mathematic18videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - CHEMISTRY SECTION-II8videos
TEST PAPER
- BOOK - ALLENCHAPTER - VECTOR ALGEBRAEXERCISE - All Questions1videos
VECTOR ALGEBRA
Similar Questions
Let A=[aij] be 3×3 matrix given by aij=⎧⎪ ⎪⎨⎪ ⎪⎩(i+j2)+|i−j|2ifi≠jij−(i.j)i2+j2ifin=j
where aij denotes element of ith row and jth column of matrix A.
On the basis of above information answer the following question:
If a 3×3 matrix B is such that A2+B2=A+B2A, then det. (√2BA−1) is equal toView SolutionConstruct a 3×2 matrix whose elements ar given by aij=12(i−3j)
View SolutionIf A=[aij] is a 2×2 matrix such that aij=i+2j , write A .
View SolutionConstruct a 2×3 matrix whose elements are given by
aij=12(i−2j)2.View SolutionConstruct a 3×2matrix whose elements are given by aij=12|i−3j|.
View SolutionConstruct a 2 * 2 matrix, A = [aij], whose elements are given by: aij=(i+j)22
View SolutionFor 2x3 matrix A=[aij] whose elements are given by aij=(i+j)22 then A is equal to
View SolutionThe square matrix A=[aij given by aij=(i−j)3, is a
View SolutionConstruct a 2×2 matrix A=[aij] whose elements are given by :
aij=(i+j)22View SolutionConstruct a 2×3 matrix A=[aij] whose elements are given by aij=i−ji+j .
View Solution