Let
be a triangle and
be two points on side
such that
If
and
THEN PROVE THAT
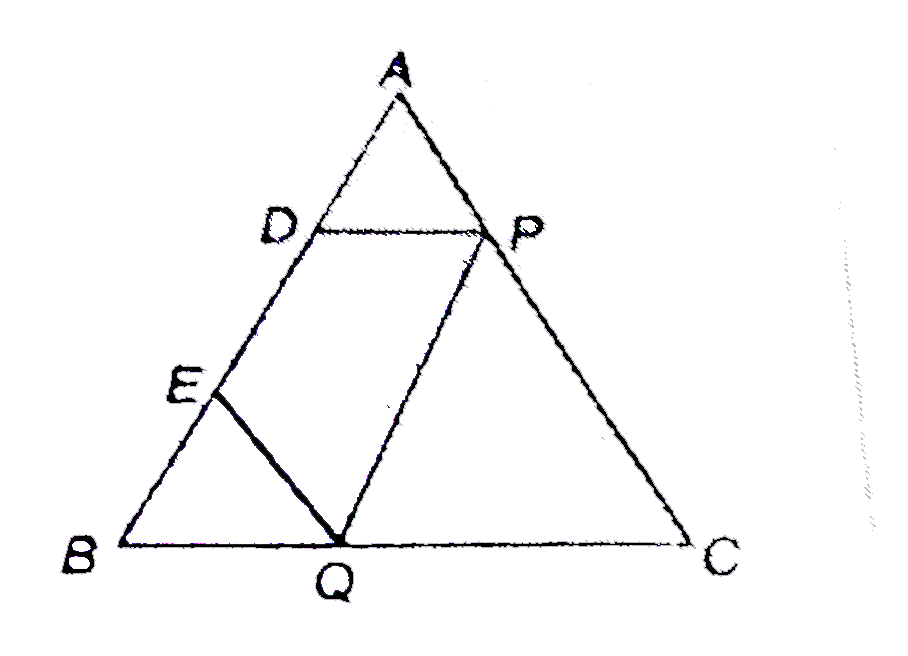
in which D and E are two points such that AD=BE.
Also DP||BC and EQ||AC.
To Prove : PQ||AB
Proof: In Since DP|| BC.
In since EQ||AC
Now, as AD=BE
AD+DE= BE+DE
AE=BD (adding DE on both sides)
AE=BD ....(4)
From (1) (2) (3) and (4)
PQ||AB ( by the converse of B.P. theroem) Hence proved.

Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a
23 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
ABCD is a trapezium in which ABDC . P and Q are points on sides AD and BC such that PQAB . If PD=18 , BQ=35 and QC=15 , find AD .
View SolutionABC is a triangle, P is a point on ABandQ is a point on AC such that ∠AQP=∠ABC. Complete the relation AreaofAPQAreaofABC=.()AC2 .
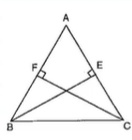
View SolutionIn Figure, BD and CE are two altitudes of a ABC such that BD=CE. Prove that ABC is isosceles.
View SolutionABC is a triangle. D is a point on AB such that D=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC
View SolutionIn ABC , P and Q are points on sides AB and AC respectively such that PQBC . If AP=4cm, PB=6cm and PQ=3cm , determine BC .
View SolutionIn Figure, ABC is a triangle in which ∠B=2∠C . D is a point on side BC such that AD bisects ∠BAC and AB=CD.BE is the bisector of ∠B . The measure of ∠BAC is
(a) 720
(b) 730
(c) 740
(d) 960

View SolutionIn a triangle ABC , let PandQ be points on ABandAC respectively such that PQ∣∣BC . Prove that the median AD bisects PQ.
View SolutionIn a ABC , P and Q are point on the sides AB and AC respectively, such that PQBC . If AP=2.4cm , AQ=2cm , QC=3cm and BC=6cm , find AB and PQ .
View SolutionLet ABC be an isosceles triangle with AB=AC and let D, E, F be the mid points of BC, CA and AB respectively. Show that AD⊥FE and AD is bisected by FE
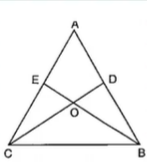
View SolutionIn Figure, it is given that AE=AD and BD=CE. Prove that AEB≅ADC
View Solution
