Let a relation R1 on the set R of real numbers be defined as (a,b)∈R⇔1+ab>0 for all a,b∈R. Show that R1 is reflexive and symmetric but not transitive.
R1={(a,b)∈R⇔1+ab>0
First we will check R for reflexive.
For, (a,a)∈R,
⇒1+a2>0, which is true.
So, R is reflexive.
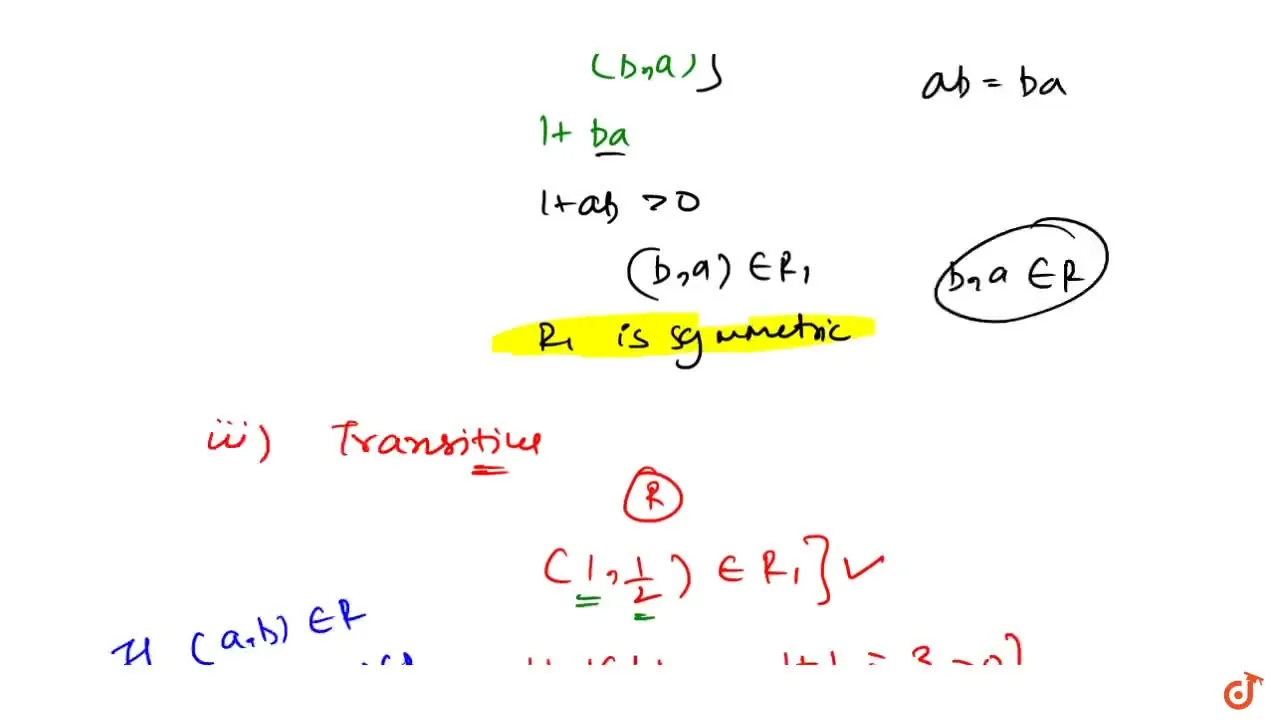
Now, we will check for symmetric.
For, (a,b)∈R,
⇒1+ab>0
⇒1+ba>0
⇒(b,a)∈R
So, R is symmetric.
Now, we will check R fo transtivity.
For, (a,b)∈Rand(b,c)∈R
⇒1+ab>0and1+bc>0
But, it is does not imply that 1+ac>0.
So, (a,c)∉R .
∴R is not transitive.
Related Playlists
Similar Questions
Let a relation R1 on the set R of real numbers be defined as (a,b)∈R⇔1+ab>0 for all a,b∈R. Show that R1 is reflexive and symmetric but not transitive.
View SolutionLet a relation R1 on the set R of real numbers be defined as (a, b)∈R1⇔1+ab>0 for all a, b∈R . Show that R1 is reflexive and symmetric but not transitive.
View SolutionThe relation R, in the set of real number defined as R={(a,b):a<b} is:
View SolutionLet R be the relation on the set R of all real numbers defined by a Rb Iff |a−b|≤1. Then R is
View SolutionLet R be the relation on the set R of all real numbers defined by a Rb Iff |a−b|≤1. Then R is
View SolutionLet R be the relation on the set R of all real numbers, defined by a→b if |a−b|≤1. Then, R is
View SolutionLet R be a relation on the set of all real numbers defined by xRy⇔|x−y|≤12 Then R is
View SolutionLet S be the set of all points in a plane and R be a relation on S defines as R={(P,Q): distance between PandQ is less than 2 units} Show that R is reflexive and symmetric but not transitive.
View SolutionLet R be the relation on the set of all real numbers defined by aRb iff |a-b|<=1 .Then R is Reflexive and transitive but not symmetric Reflexive symmetric and transitive Symmetric and transitive but not reflexive Reflexive symmetric but not transitive
View SolutionLet R be the relation on the set of all real numbers defined by aRb iff |a-b|<=1 .Then R is O Reflexive and transitive but not symmetric O Reflexive symmetric and transitive O Symmetric and transitive but not reflexive O Reflexive symmetric but not transitive
View Solution