Let ABCD be a parallelogram the equation of whose diagonals are $A C : x + 2 y = 3$ ; BD: 2x + y = 3. If length of diagonal $A C = 4$ units and area of $A B C D = 8$ sq. units. (i) The length of the other diagonal is (ii) the length of side AB is equal to

A

$10 / 3$

B

2

C

$20 / 3$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

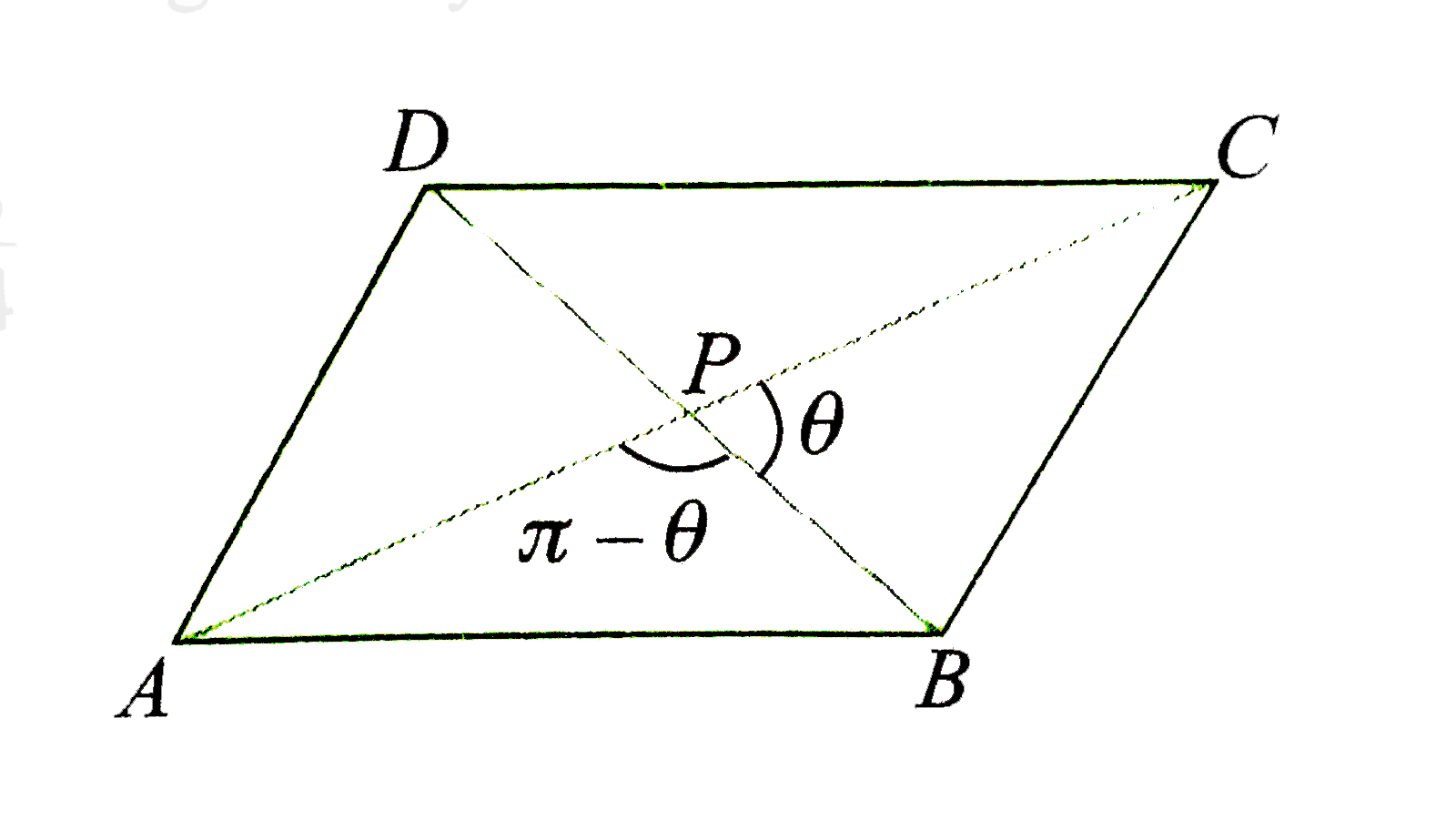
Angle between the diagonal is given by
$tan θ = ∣ ∣ ∣ ∣ \frac{- \frac{1}{2} + 2}{1 + 1} ∣ ∣ ∣ ∣ = \frac{3}{4}$
$or sin θ = \frac{3}{5}$
Area of $Δ C P B$ is
$\frac{1}{2} \times P C \times P B sin θ = 2$
or $P B = \frac{10}{3}$
or $B D = \frac{20}{3}$

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let ABCD be a parallelogram whose equations for the diagonals AC and BD are x+2y=3 and 2x+y=3, respectively.
The length of side AB is equal to
A $2 \sqrt{58} / 3$
B $4 \sqrt{58} / 9$
C $3 \sqrt{58} / 9$
D $4 \sqrt{58} / 9$
Question 2 - Select One
If the length of the diagonal AC of a square ABCD is 5.2 cm, then the area of the square is :
A15.12 sq. cm
B13.52 sq. cm
C12.62 sq. cm
D10.00 sq. cm.
Question 3 - Select One
If the length of the diagonal AC of a square ABCD is 5.2 cm, then the area of the square is :
A15.12 sq . Cm
B13.52 sq. cm
C12.62 sq. cm
D10 sq. cm

CENGAGE-STRAIGHT LINES-Exercise (Comprehension)

Home
Ask Doubt
Profile