Let F and G be two real-valued function defined on R (the set of all real numbers)
F(x)={|x+1|x{:(,xle0,),(,xgt0,):}G(x)={:{(,|x|+1,),(,-|x-2,):}x≤1x>1 and H(x)=F(x)+G(x).
Point of discontinuity of H(x) are
x=0
x=1
x=2
x=−1
The correct Answer is:A, B
We have, F(x)=⎧⎪⎨⎪⎩−(x+1)(x+1)(x)x<−1−1≤x≤0x>0
and G(x)=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩−x+1x+1x−22−x−∞<x≤00<x≤11<x<2x≥2
H(x)=F(x)+G(x)=⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩−(x−1−x+1=−2x)(x+1)−x+1=2x+(x+1)=2x+1x+(x−2)=2x−2x+2−x=2−∞<x≤−1−1≤x≤00≤x≤11<x<2x≥2
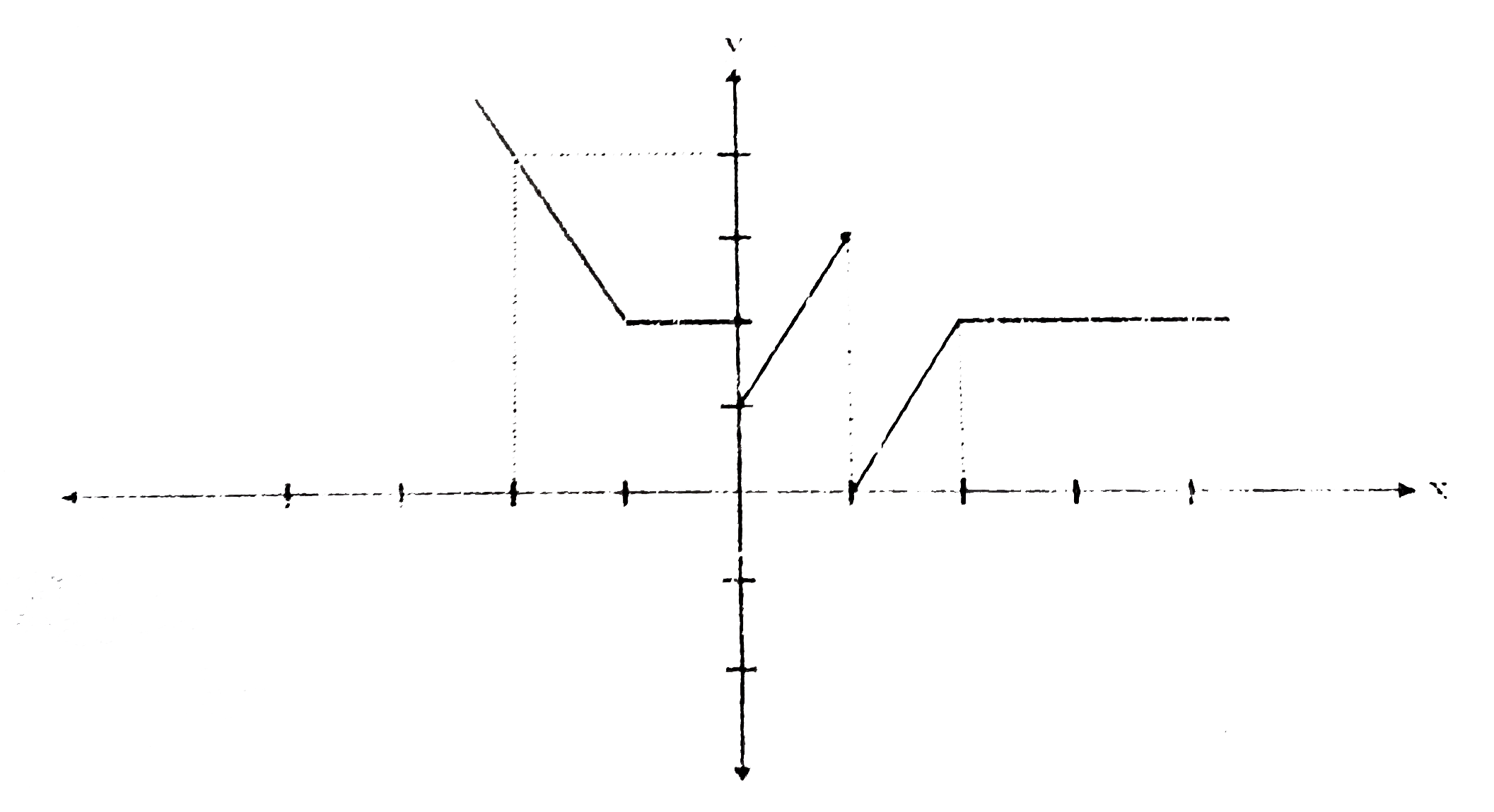 Graph of H(x)
Graph of H(x)
Clearly from the graph, H(x) is discontinous at
x=0 and x=1, i.e., 2 points of discontinuity
∴A&B
Graphically,
Area under curve from −2→2
=(12×2×1×1)+(2+1)+(12×2×1×1)+(12×2×1)
=(1+2)+2+(1+1)+1
=3+2+2+1=8
Related Playlists
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHEMATICS51videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - CHEMISTRY1videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 Mathematic18videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - CHEMISTRY SECTION-II8videos
TEST PAPER
- BOOK - ALLENCHAPTER - VECTOR ALGEBRAEXERCISE - All Questions1videos
VECTOR ALGEBRA
Similar Questions
Let F and G be two real-valued function defined on R (the set of all real numbers)
F(x)={|x+1|x{:(,xle0,),(,xgt0,):}G(x)={|x|+1−∣x−2{:(,xle1,),(,xgt1,):}andH(x)=F(x)+G(x).<br>Thevalueofdef∈ite∫egralint_(-2)^(2) H(x) dx is equal toView SolutionLet f and g be two real valued functions ,defined by f(x) =x ,g(x)=[x]. Then find the value of f+g
View SolutionLet f and g be two real values functions defined by f(x)=x+1 and g(x)=2x−3. Find 1) f+g, 2) f−g, 3) fg
View Solutionlet f(x) =√x and g(x) =x be function defined over the set of non negative real numbers . find (f+g)(x),(fg)(x)and(fg)(x) .
View SolutionLet f(x)={1+x0≤x≤23−x2<x≤3, then the points of discontinuity of g(x)=f[f(x)] is/are
View SolutionA function is defined as f(x)={ex,x≤0|x−1|,x>0, then f(x) is
View SolutionLet f(x),g(x) be two real valued functions then the function h(x)=2max{f(x)−g(x),0} is equal to :
View SolutionLet f and g real functions defined by f(x)=2x+1 and g(x)=4x−7.
(i) For what real number x,f(x)=g(x)?
(ii) x,f(g)<g(x)?View SolutionIf f(x)={x2x≤0xx>0 and g(x)=−|x|,x∈R, then find fog and gof.
View SolutionLet f(x)=√xand g(x)=xbe two functions defined over the set of nonnegative real numbers. Find (f+g)(x), (fg)(x), (fg)(x)and (fg)(x).
View Solution


