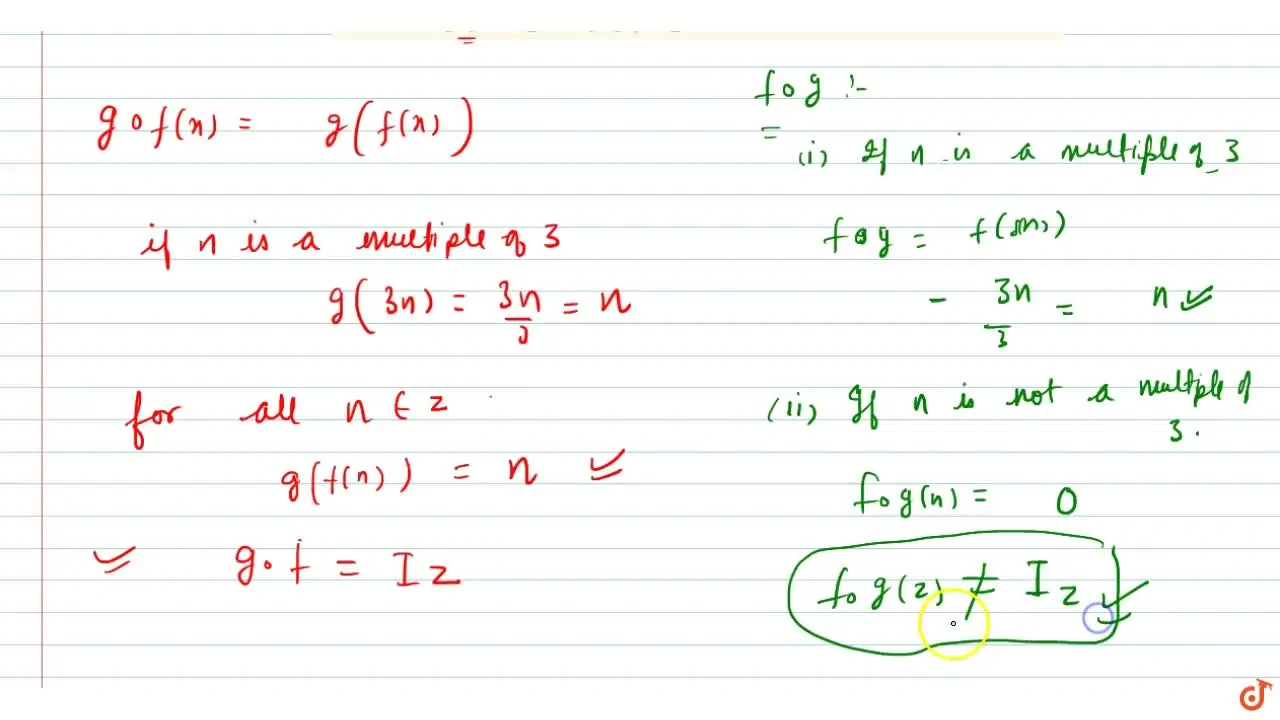Let f:Z→Z be defined by f(n)=3n for all n∈Z and g:Z→ be defined by f(n)={n3,ifnisaμltipleof30,ifnis¬μltipleof3foralln∈Z. Show that gof=IZ and fog≠IZ
Let n be an arbitrary element of Z. Then
(gof)(n)=g{f(n)}
=g(3n)=3n3=n
=IZ(n)
∴(gof)=IZ
Also we have
(fog)(1)=f{g(1)}
=f(0)[∵g(1)=0]
=(3×0)=0[∵f(n)3n]
IZ(1)=1[∵IZ(x)=∀x∈Z]
∴fog≠IZ
Related Playlists
- BOOK - RS AGGARWALCHAPTER - FUNCTIONSEXERCISE - Objective Questions39videos
FUNCTIONS
- BOOK - RS AGGARWALCHAPTER - FUNCTIONSEXERCISE - Exercise 2A17videos
FUNCTIONS
- BOOK - RS AGGARWALCHAPTER - DIFFERENTIATIONEXERCISE - Exercise 10I51videos
DIFFERENTIATION
- BOOK - RS AGGARWALCHAPTER - FUNDAMENTAL CONCEPTS OF 3-DIMENSIONAL GEOMETRYEXERCISE - Exercise18videos
FUNDAMENTAL CONCEPTS OF 3-DIMENSIONAL GEOMETRY
Similar Questions
If f:Z→Z be defined by f(x)=2x for all x∈Z . Find g:Z→Z such that gof=IZ .
View SolutionLet f:Z→Z be defined by f(x)=x+2. Find g:Z→Z such that gof=IZ .
View SolutionLet f:N∪{0}→N∪{0} be defined by f{n+1,ifn is even n-1,if n is odd Show that f is a bijection.
View SolutionLet f:N→N be defined by f(n)={n+12, if n i s\ o d dn2, if\ n i s\ e v e n for all n N} Find whether the function f is bijective.
View SolutionLet f:R→R be defined by f(x)=x2+3x+1 and g:R→R is defined by g(x) = 2x - 3, Find,
(i) fog
(ii) gofView SolutionLet N→N be defined by f(x) = 3x. Show that 'f' is not an onto function.
View SolutionLet f:N→Z be a function defined as f(x)=x−1000. Show that f is an into function.
View SolutionLet f:N∪{0}→N∪{0} be defined by f(n)={n+1, if n is even, n−1, if n is odd Show that f is invertible and f=f−1 .
View SolutionLet f be a relation on the set N of natural numbers defined by f={(n,3n):n∈N} is f a function from N → N . If so, find the range of f .
View SolutionIs the function f:N→N (N is set of the natural numbers) defined by f(n) = 2n +3 for all n∈N surjective ?
View Solution