Let F:[3,∞]→[1,∞] be defined by f(x)=πx(x−3), if f−1(x) is inverse of f(x) then the number of solution of the equation f(x)=f−1(x) are
The correct Answer is:1
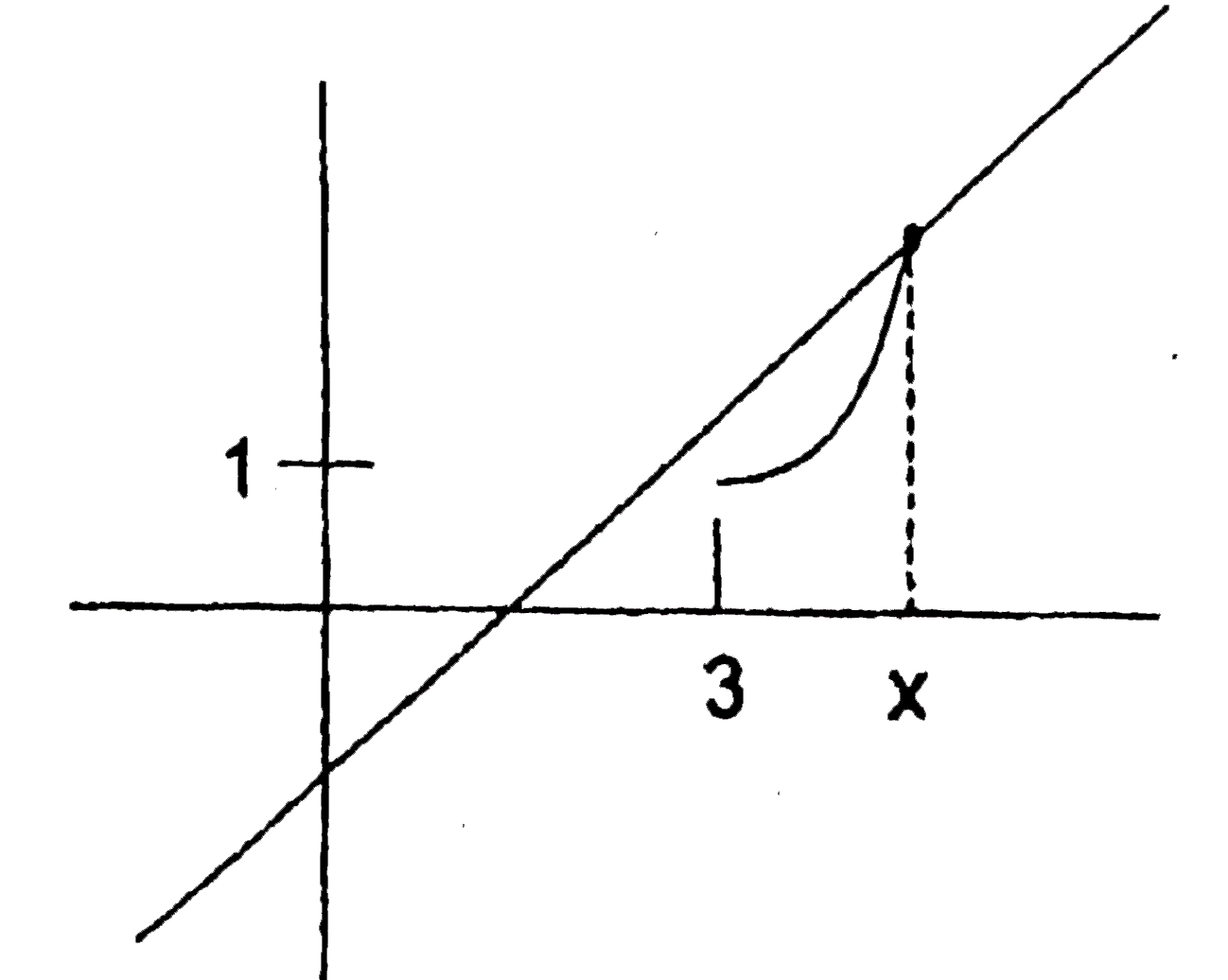
f(x)=πx(x−3):[3,∞]→[1,∞]
solution of f(x)=f−1(x) lies on line y=x
for x∈[3,∞] the function
f(x)=πx(x−3) is strictly increasing and intersect the line y
=x at only one point
f(x)=f−1(x) has only one solution
Related Playlists
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - MATHEMATICS263videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - I MATHMATICS84videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPEREXERCISE - CHEMISTRY37videos
TEST PAPER
- BOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - MATHEMATICS131videos
TEST SERIES
Similar Questions
Let f(x)=2x+1.∀x, then the solution of the equation f(x)=f−1(x) is
View SolutionIf f(x)=2x−1 then number of solution (s) of the equation |f(x)|=|f(|x|−1)| is (are)
View SolutionLet f(x)=x+sinx. Find the number of solutions of f(x)=f−1(x)
View SolutionLet f(x)−2x−x2,x≤1 then the roots of the equation f(x)=f−1(x) is
View SolutionIf f(x)=−x3, then all the solutions of the equation f(x)=f−1(x) lie on the line
View SolutionLet f:[4,∞)→[1,∞) be defined by
f(x)=11x(4−x)∀x≥4
Then f−1(x) is given byView SolutionIf f(x)={0,x<1and2x−2,x≤1 then the number of solutions of the equation f(f(f(x)))=x is
View SolutionLet f(x)=x2−x+1,∀x≥12, then the solution of the equation f(x)=f−1(x) is
View SolutionLet f:(1→∞)→(1,∞) be defined by f(x)=x+2x−1. Then
View SolutionLet the function f be defined by f(x)=(2x+11−3x) then f−1(x) is
View Solution


