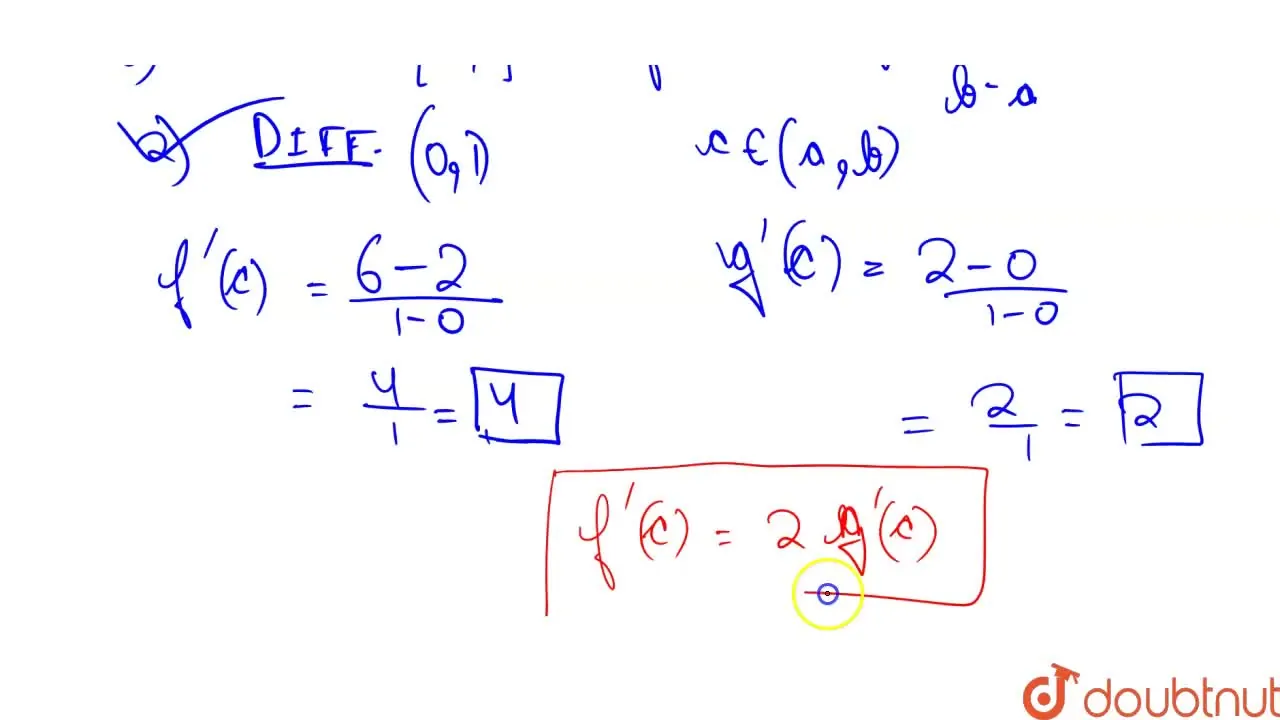Let fandg be differentiable on [0,1] such that f(0)=2,g(0)=0,f(1)=6andg(1)=2. Show that there exists c∈(0,1) such that f′(c)=2g′(c).
The correct Answer is:Proved
Since f and g are differentiable functions for the interval [0,1]
∴ they are also continuous for the interval [0,1] Consequently by LMV Theorem,
For f(x),
$$
f^{\prime}(c)=\frac{f(1)-f(0)}{1-0}=\frac{6-2}{1}=4 \quad-(1)
$$
For $g(x)$
$$
g^{\prime}(c)=\frac{g(1)-g(0)}{1-0}=\frac{2-0}{1}=2-(2)
$$
Divide (1) by (2), we get
$$
\begin{aligned}
&\frac{f^{\prime}(c)}{g^{\prime}(c)}=\frac{4}{2}=2 \\
&\therefore f^{\prime}(c)=2 g^{\prime}(c) \\
&\therefore \quad f \text { exists } c \in(0,1)
\end{aligned}
$$
Related Playlists
Similar Questions
Let fandg be differentiable on [0,1] such that f(0)=2,g(0)=0,f(1)=6andg(1)=2. Show that there exists c∈(0,1) such that f′(c)=2g′(c).
View SolutionLet y=f(x) and =g(x) be two differentiable function in [0,2] such that f(0)=3,f(2)=5,g(0)=1 and g(2)=2. If there exist at least one c∈(0,2) such that f'(c)=kg'(c) then k must be
View SolutionLet f(x)andg(x) be differentiable for 0≤x≤1, such that f(0)=0,g(0)=0,f(1)=6. Let there exists real number c in (0,1) such taht f′(c)=2g′(c). Then the value of g(1) must be 1 (b) 3 (c) −2 (d) −1
View SolutionIf f(x) and g(x) ar edifferentiable function for 0≤x≤1 such that f(0)=2,g(0)=0,f(1)=6,g(1)=2, then in the interval (0,1)
View SolutionIf f is a continuous function on [0,1], differentiable in (0, 1) such that f(1)=0, then there exists some c∈(0,1) such that cf′(c)−f(c)=0 cf′(c)+cf(c)=0 f′(c)−cf(c)=0 cf′(c)+f(c)=0
View SolutionLet f(x)andg(x) be differentiable for 0≤x≤2 such that f(0)=2,g(0)=1,andf(2)=8. Let there exist a real number c in [0,2] such that f′(c)=3g′(c). Then find the value of g(2).
View SolutionLet f(x) and g(x) be differentiable for 0<=x<=1 such that f(0)=0 g(0)=6 .let there exists a real number c in (0 1) such that f'(c)=2g'(c) then the value of g(1) must be
View Solutionf(x) and g(x) are differentiable functions for 0≤x≤2 such that f(0)=5,g(0)=0,f(2)=8,g(2)=1. Show that there exists a number c satisfying 0<c<2 and f'(c)=3g'(c).
View SolutionIf f be a continuous function on [0,1] differentiable in (0,1) such that f(1)=0, then there exists some c∈(0,1) such that
View SolutionIf f and g are differentiable function in [0, 1] satisfying f (0) = 2 = g(1), g(0) = 0 and f (1) = 6, then for some c∈(0,1)
View Solution