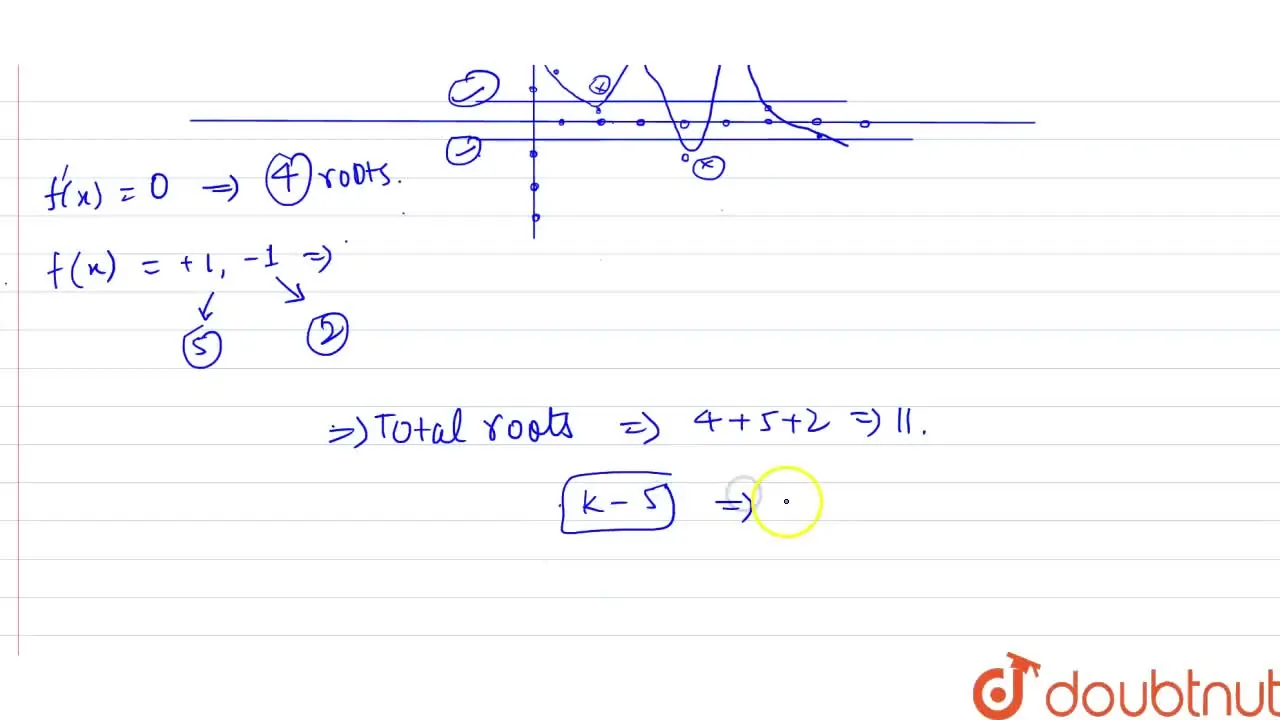
Let f(x) be a differentiable function on [0,8] such that f(1)=3,f(2)=1/2,f(3)=4,f(4)=−2,f(5)=6
f(6)=1/3,f(7)=−1/4. Then the minimum no. points of interaction of the curve y=f′(x) and y=f′(x)(f(x))2 is K then K−5=
The correct Answer is:6
f′(x)=f′(x)(f(x))2
Either f′(x)=0 at least 4 roots
f(x)=1 at least 5 roots
f(x)=−1 at least 2 roots
at least 11 roots.

Related Playlists
Similar Questions
If f(x) is a twice differentiable function and given that f(1) = 1, f(2) = 4, f(3) = 9, then
View SolutionLet y=f(x) be a differentiable function such that f(−1)=2,f(2)=−1 and f(5)=3 then the equation f'(x)=2f(x) has
View Solutionf (x) is twice differentiable polynomial function such that f (1) = 1, f (2) = 4, f (3)=9, then
View SolutionIf f(x) be a differentiable function, such that f(x)f(y)+2=f(x)+f(y)+f(xy);f'(0)=0,f(1)=2 then find f(x).
View SolutionIf f(x) is a quadratic function such that f(0)=3,f(1)=6andf(2)=11, then: f(x)=
View SolutionLet f(x) be a function differentiable on [0,a] such that f(0)=1,f(a)=31/6
If f'(x)≥[f(x)]4+[f(x)]−2 , then the maximum value of a isView SolutionIf f is twice differentiable function for x∈R such that f(2)=5,f'(2)=8 and f'(x)≥1,f''(x)≥4 , then
View SolutionLet f(x) be a differentiable function satisfying f(x+2y3)=f(x)+2f(y)3∀x,y∈R and f′(0)=1, f(0) =-1. Then the number of points where |f(|x|)| is non-derivable is
View SolutionLet f(x) be a differentiable function satisfying f(y)f(xy)=f(x) ∀, x,y∈R, y≠0 and f(1)≠0, f'(1)=3 then
View SolutionLet f be a differentiable function such that 8f(x)+6f(1/x)−x=5(x≠0) and y=x2f(x), then dydx at x = 1 is
View Solution