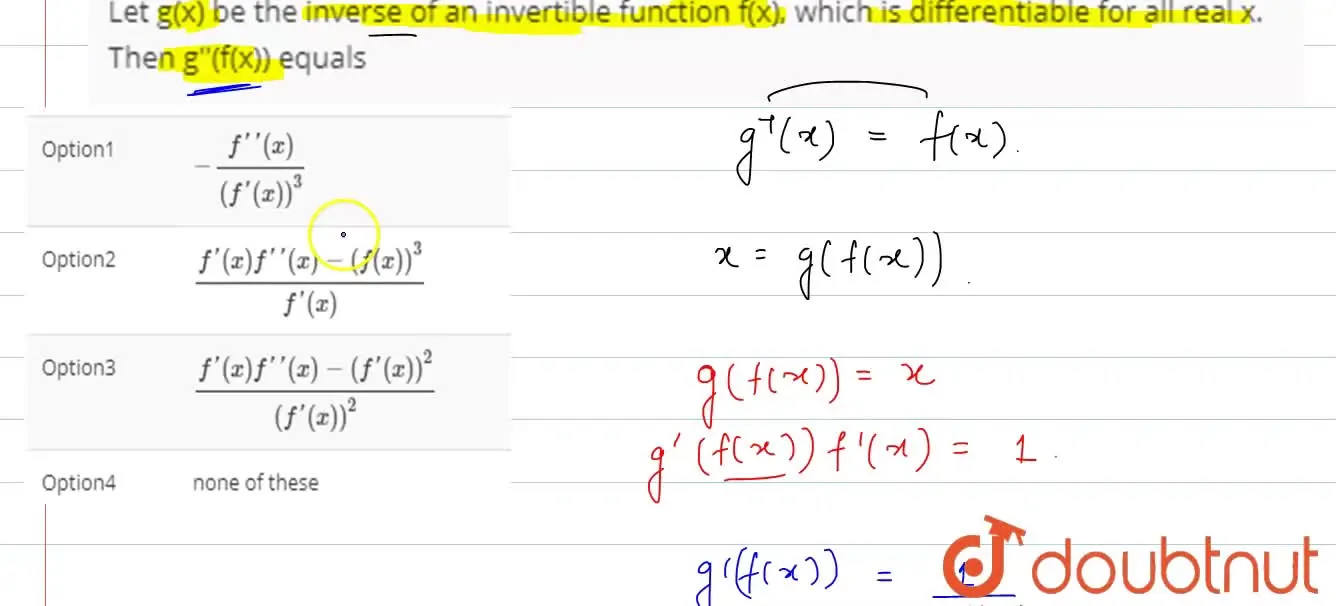
Let g(x) be the inverse of an invertible function f(x), which is differentiable for all real x. Then g''(f(x)) equals
−f''(x)(f'(x))3
f'(x)f''(x)−(f(x))3f'(x)
f'(x)f''(x)−(f'(x))2(f'(x))2
none of these
Given that g−1(x)=f(x)
or x=g(f(x))
or g'(f(x))f'(x)=1
or g'(f(x))=1f'(x)
or g''(f(x))f'(x)=−f''(x)[f'(x)]2
or g''(f(x))=−f''(x)[f'(x)]3
Related Playlists
- BOOK - CENGAGECHAPTER - DIFFERENTIATIONEXERCISE - Exercise (Multiple)22videos
DIFFERENTIATION
- BOOK - CENGAGECHAPTER - DIFFERENTIATIONEXERCISE - Exercise (Comprehension)23videos
DIFFERENTIATION
- BOOK - CENGAGECHAPTER - DIFFERENTIATIONEXERCISE - Exercise 3.914videos
DIFFERENTIATION
- BOOK - CENGAGECHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Question Bank25videos
DIFFERENTIAL EQUATIONS
- BOOK - CENGAGECHAPTER - DOT PRODUCTEXERCISE - DPP 2.115videos
DOT PRODUCT
Similar Questions
Let g(x) be the inverse of an invertible function f(x), which is differentiable for all real x. Then g''(f(x)) equals. (a)−f''(x)(f′(x))3 (b) f′(x)f''(x)−(f′(x))3f′(x) (c)f′(x)f''(x)−(f′(x))2(f′(x))2 (d) none of these
View SolutionLet g(x) be the inverse of an invertible function f(x), which is differentiable for all x, then g''f(x) is equal to
View SolutionLet g(x) be the inverse of an invertible function f(x) which is differentiable at x=c . Then g′(f(x)) equal. (a)f′(c) (b) 1f′(c) (c) f(c) (d) none of these
View SolutionLet g(x) be the inverse of an invertible function f(x) which is derivable at x=3 . If f(3)=9 and f′(3)=9 , write the value of g′(9) .
View SolutionA function f(x) is differentiable at x=c(c∈R). Let g(x)=|f(x)|,f(c)=0 then
View SolutionLet g(x) be the inverse of the function f(x) ,and f'(x)11+x3 then g(x) equals
View SolutionLet g(x) be the inverse of the function f(x), and f'(x)=11+x3 then g'(x) equals
View SolutionLet g(x) be the inverse of the function f(x) ,and f'(x)11+x3 then g(x) equals
View SolutionLet g(x) be the inverse of the function f(x)=lnx2,x>0. If a,b,c∈R ,then g(a+b+c) is equal to
View SolutionLet f(x) be differentiable function and g(x) be twice differentiable function. Zeros of f(x),g′(x) be a,b , respectively, (a<b). Show that there exists at least one root of equation f′(x)g′(x)+f(x)gx=0 on (a,b).
View Solution