Let I be any interval disjoint from (1,1). Prove that the function f given by f(x)=x+1xis strictly increasing on 1.
Video Solution
Text Solution
f(x)=x+1x,x≠0
⇒f'(x)=1−1x2=x2−1x2=(x−1)(x+1)x2
If f'(x)=0 then (x−1)(x+1)=0
⇒x=1,−1
Now, divide R into intervals (−∞,−1),(−1,1)and(1,∞).
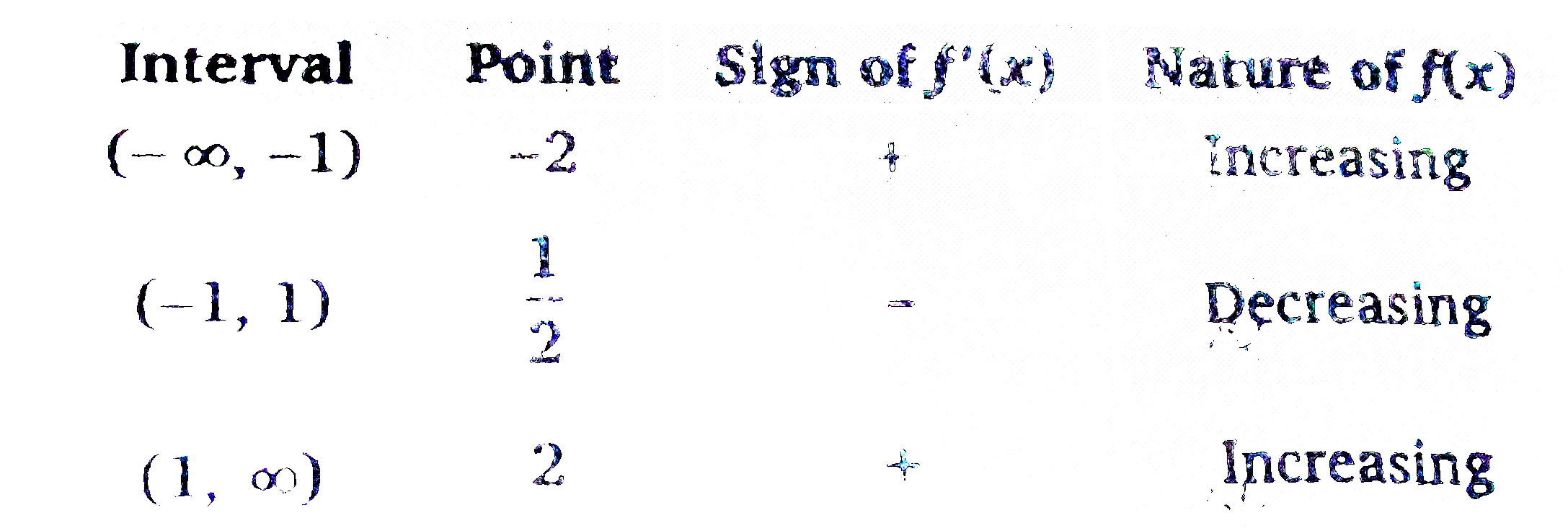
∴f(x) is increasing in I=(−∞,−1)∪(1,∞).
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6.327videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6.49videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6.118videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Miscellaneous Exercise19videos
APPLICATIONS OF INTEGRALS
Similar Questions
Knowledge Check
- Question 1 - Select One
The function f(x)=x2−2x is strictly increasing in the interval
A(-2, -1)B(-1, 0)C(0, 1)D(1, 2)
Prove that the function f given by f(x)=x−[x] is increasing in (0, 1) .
View SolutionLet I be an interval disjointed from [−1, 1] . Prove that the function f(x)=x+1x is increasing on I .
View SolutionProve that the function f(x)=10x is strictly increasing on R
View SolutionShow that the function f(x)=ax, a>1 is strictly increasing on R.
View SolutionShow that the function f(x) = 2x+1 is strictly increasing on R.
View SolutionProve that the function f(x)=[x]−x is strictly decreasing on [0,1).
View SolutionProve that the function f(x)=(log)e(x2+1)−e−x+1 is strictly increasing ∀x∈R.
View Solution

