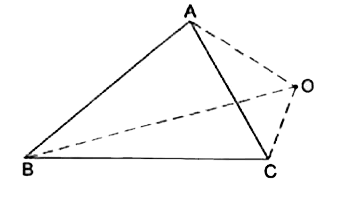
Let O be an interior point of △ABC such that −−→OA+2−−→OB+3−−→OC=→o . Then find the ratio of the area of △ABC to the area of △BRC is 1 unit. Solution in Tamil
2
32
3
52
The correct Answer is:C

−−→OD=→a+→2b3=−→a, (∴→a+→2b+→3c=→0)
⇒|OD|=|OC|
Now (ar(△ACD))(ar(△BCD))=2
⇒ar(△ACD)=2Δ3, where Δ is area of △ABC
ar(△AOC)=12ar(△ACD)
=12×2Δ3=Δ3
⇒ar(△ABC)ar(△AOC)=3
Topper's Solved these Questions
Similar Questions
→a=2ˆi+ˆj+ˆk, →b=b1ˆi+b2ˆj+b3ˆk,
→a×→b=5ˆi+2ˆj−12ˆk,→a.→b=11, then b1+b2+b3=10:23View SolutionLet O be an interior point of Delta ABC such that 2vec OA+5vec OB+10vec OC=vec 0
01:27View SolutionIf 2→AC = 3→CB , then prove that 2→OA =3→CB then prove that 2→OA + 3→OB =5→OC where O is the origin.
05:33View SolutionLet O be an interior point of DeltaABC such that bar(OA)+2bar(OB) + 3bar(OC) = 0. Then the ratio of a DeltaABC to area of DeltaAOC is
03:48View SolutionLet −−→OA=→a,−−→OB=10→a+2→b & −−→OC=→b , where O,A,C are non-collinear. Let 'p' denote area of quadrilateral OABC & 'q' denote area of parallelogram with OA & OC as adjacent sides, then pq=
03:43View SolutionIf O is point in the exterior of △ABC,show that 2(OA+OB+OC)>(AB+BC+CA)
 03:35View Solution
03:35View SolutionLet O be an interior point of triangle ABC, such that 2−−→OA+3−−→OB+4−−→OC=0, then the ratio of the area of ΔABC to the area of ΔAOC is
01:59View Solution¯¯¯¯¯¯AB রেখাংশের মধ্যবিন্দু C এবং O যে-কোন বিন্দু ( AB-র ওপর অবস্থিত নয় ) হলে প্রমাণ করো যে, −−→OA+−−→OB=2−−→OC |
03:48View SolutionLet O be an interior point of ΔABC such that ¯¯¯¯¯¯OA+2¯¯¯¯¯¯OB+3¯¯¯¯¯¯OC=0. Then the ratio of a ΔABC to area of ΔAOC is
06:32View SolutionLet O be an interior point of ΔABC such that ¯¯¯¯¯¯OA+2¯¯¯¯¯¯OB+3¯¯¯¯¯¯OC=0. Then the ratio of a ΔABC to area of ΔAOC is
03:23View Solutionयदि −−→OA=→a,−−→OB=10→a+2→b तथा −−→OC=→b हो, जहाँ O, A तथा C असमतीय बिंदु हैं यदि p चतुर्भुज OACB के क्षेत्रफल को प्रदर्शित करें तथा आसन्न भुजाओं OA तथा OC वाले समान्तर चतुर्भुज के क्षेत्रफल को q से प्रदर्शित किया जाता है, यदि p=kq है, तब k ज्ञात करो
05:20View SolutionLet −−→OA=→a,−−→OB=10→a+2→b and −−→OC=→b where O is origin. Let P denotes the area of the quadrilateral OABC and q denote the area of the parallelogram with OA and OC as adjacent side. Prove that P = 6q.
05:05View SolutionLet −−→OA=→a,−−→OB=10→a+2→b,−−→OC=→b where O, A, C are non-collinear points. Let λ denote the area of the quadrilateral OABC and let μ denote the area of parallelogram with −−→OAand−−→OC as ajacent sides show that λ=6μ
04:40View Solution−−→OA=→a,−−→OB=10→a+2→b,−−→OC=→b where O, A, C are non-collinear points. Let 'p' denote area of quadrilateral OABC, 'q' denote area of parallelogram with OA, OC as adjacent sides, then pq=
06:20View SolutionLet O be an interior point of triangle ABC, such that 2−−→OA+3−−→OB+4−−→OC=0, then the ratio of the area of ΔABC to the area of ΔAOC is
06:55View SolutionLet O be an interior point of DeltaABC such that bar(OA)+2bar(OB) + 3bar(OC) = 0 . Then the ratio of a DeltaABC to area of DeltaAOC is
01:18View Solution

