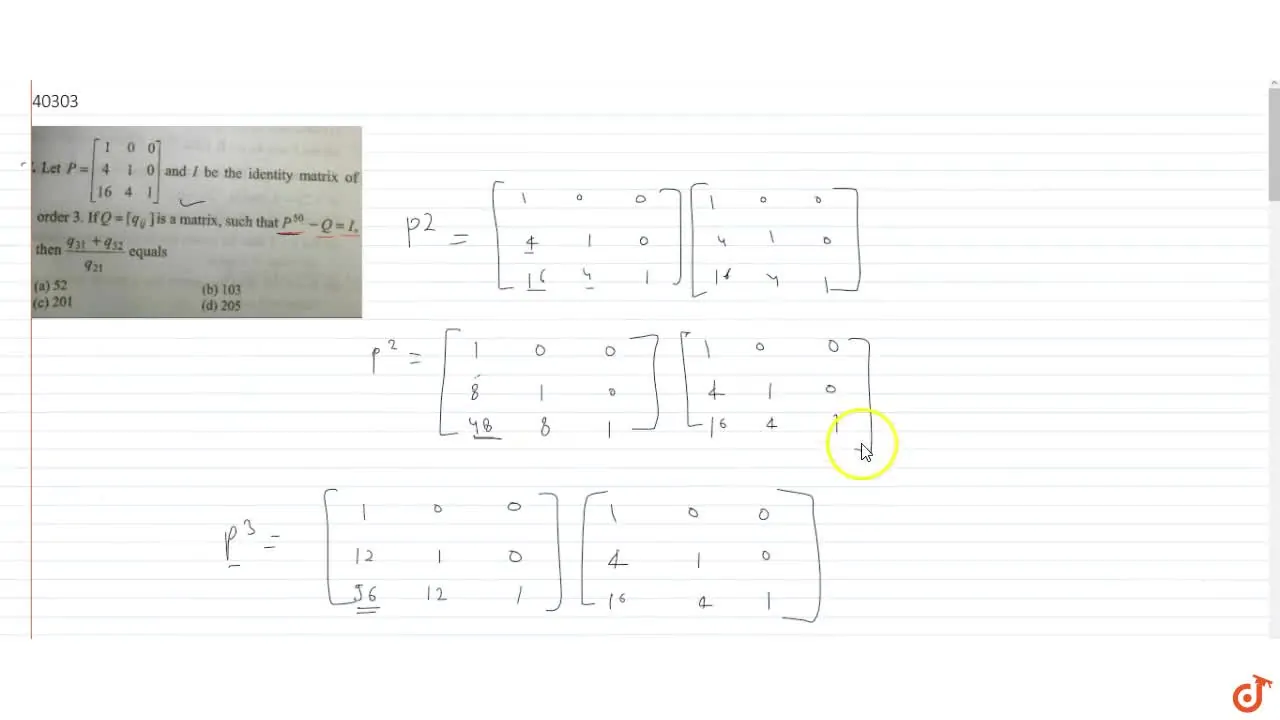
Let P=⎡⎢⎣1004101641⎤⎥⎦and I be the identity matrix of order 3. If Q=[qij] is a matrix, such that P50−Q=I, then q31+q32q21 equals
52
103
201
205
The correct Answer is:B
We have, P=⎡⎢⎣1004101641⎤⎥⎦.
∴P2=PP=⎡⎢⎣1004101641⎤⎥⎦⎡⎢⎣1004101641⎤⎥⎦=⎡⎢⎣10081016+3281⎤⎥⎦
∴P3=P2P=⎡⎢⎣10081016+3281⎤⎥⎦⎡⎢⎣1004101641⎤⎥⎦=⎡⎢⎣100121016+32+48121⎤⎥⎦
By observing the symmetry, we obtain
P50=⎡⎢⎣1004×501016+32+48+...50terms4×501⎤⎥⎦
⇒P50⎡⎢
⎢⎣1002001016×50×5122001⎤⎥
⎥⎦
∴P50−Q=I
⇒Q=P50−I⎡⎢⎣00020000204002000⎤⎥⎦
⇒q21=200,q31=20400andq32=200
∴q31+q32q21=20400+200200=20600200=103
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - MATRICESEXERCISE - Section I - Solved Mcqs57videos
MATRICES
- BOOK - OBJECTIVE RD SHARMACHAPTER - MATRICESEXERCISE - Section I - Assertion Reason Type12videos
MATRICES
- BOOK - OBJECTIVE RD SHARMACHAPTER - LOGARITHMSEXERCISE - Chapter Test21videos
LOGARITHMS
- BOOK - OBJECTIVE RD SHARMACHAPTER - MEAN VALUE THEOREMSEXERCISE - Exercise28videos
MEAN VALUE THEOREMS
Similar Questions
Let P=⎡⎢⎣1004101641⎤⎥⎦and I be the identity matrix of order 3. If Q=[qij] is a matrix, such that P50−Q=I, then q31+q32q21 equals
View Solution⎡⎢⎣235412121⎤⎥⎦=P+Q , where P is a symmetric matrix and Q is a skew symmetric matrix then Q=
View SolutionSuppose a ∈ R and a≠0 . Let
P=⎡⎢⎣100a10a2a1⎤⎥⎦ and Q=(aij)
be 3×3 matrices such that Q−P5=I3. If q21+q31q32=12.1 then a = _____View SolutionIf P=[λ071] and Q=[40−71] such that P2=Q, then P3 is equal to
View SolutionLet A=⎡⎢⎣02qrpq−rp−qr⎤⎥⎦ If AAT=I3 then |p|=
View SolutionLet P=⎡⎢⎣3−1−220α3−50⎤⎥⎦ , where α∈R . Suppose Q=[qij] is a matrix satisfying PQ=KI3 for some non - zero K∈R. If q23=−K8and|Q|=12, then α2+k2 is equal to ________.
View SolutionIf A=[60pq] is a scalar matrix then the value of p and q are
View SolutionLet A = [23a0],a∈R be written as P + Q where P is a symmetric matrix and Q is skew symmetric matrix. If det(Q) = 9, then the modulus of the sum of all possible values of determinant of P is equal to :
View SolutionLet the matrices A=[√3−201] and P be any orthogonal matrix such that Q = PAP and let R≠[r0]2−2=P'Q6Pthen
View SolutionIf the points (0,0), (3,√3 ), (p,q) form an equilateral triangle and q1,q2 are the two values of q then q1+q2=
View Solution