Let S be the set of all complex numbers satisfying .if the complex number is such that is the maximum of the set , then the principal argument of is
The correct Answer is:C
The complex number satisfying , which represents the region outside the circle (including the circumference )having centre and radius units.
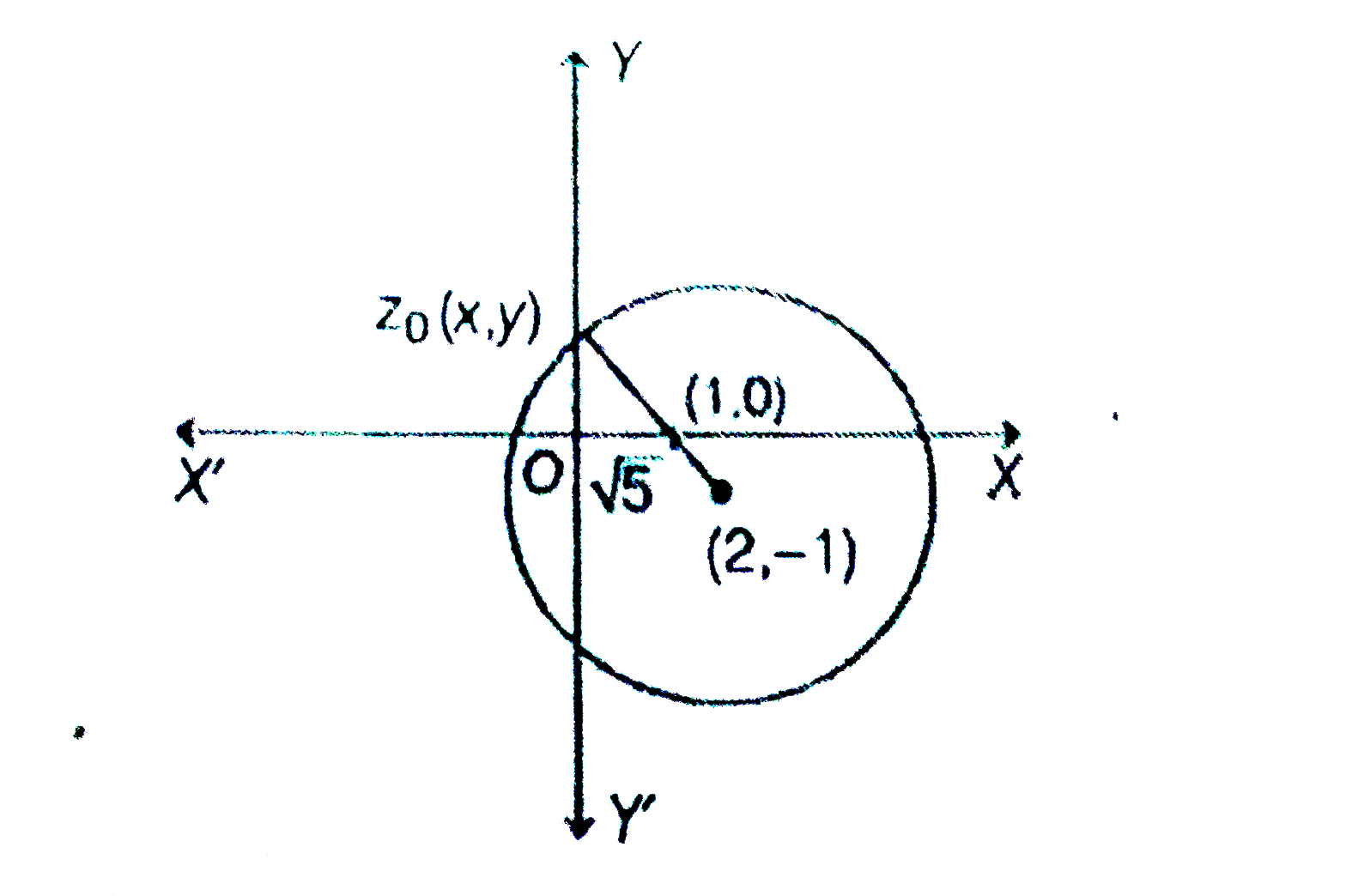
Now, for is maximum.
When is minimum. And for this it is required that is collinear with the points and and lies on the circumference of the circle .
So let , and the figure .
So,
is a positive real number, so
is purely negative imaginary number.
.
Related Playlists
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - SOLVED PAPER 2019EXERCISE - Paper -1 section-28videos
SOLVED PAPER 2019
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - SOLVED PAPER 2019EXERCISE - Paper -1 section-36videos
SOLVED PAPER 2019
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - SEQUENCES AND SERIESEXERCISE - RELATION BETWEEN AM,GM, HM AND SOME SPECIAL SERIES34videos
SEQUENCES AND SERIES
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - STRAIGHT LINE AND PAIR OF STRAIGHT LINESEXERCISE - GENERAL EQUATION OF PAIR OF STRAIGHT LINES (Objective Questions I) (Only one correct option)1videos
STRAIGHT LINE AND PAIR OF STRAIGHT LINES
Similar Questions
Find a complex number z satisfying the equation z+√2|z+1|+i=0.
View Solutionif z is a complex number belonging to the set S={z|z−2+i∣≥√5} and z0∈S such that 1|z0−1| is maximum then arg (4−z0−¯z0z0−¯z0+2i) is
View Solutionif z is a complex number belonging to the set S={z|z−2+i∣≥√5} and z0∈S such that 1|zn−1| is maximum then arg (4−z0−¯z0z0−¯z0+2i) is
View SolutionFind a complex number z satisfying the equation z+√2|z+1|+i=0.
View SolutionFind a complex number z satisfying the equation z+√2|z+1|+i=0.
View SolutionFind a complex number z satisfying the equation z+√2|z+1|+i=0.
View SolutionIF a≥1, find all complex numbers z satisfying the equation z+a|z+1|+i=0
View SolutionIF a≥1, find all complex numbers z satisfying the equation z+a|z+1|+i=0
View SolutionLet s be the set of all complex numbers Z satisfying ∣∣z2+z+1∣∣=1. Then which of the following statements is/are TRUE?
View SolutionThe complex number z satisfying the equation |z−i|=|z+1|=1
View Solution

