Let S is the focus of the parabola y2=4ax and X the foot of the directrix, PP' is a double ordinate of the curve and PX meets the curve again in Q. Prove that P'Q passes through focus.
A
line
B
circle
C
parabola
D
none of these
Video Solution
Text Solution
The correct Answer is:A
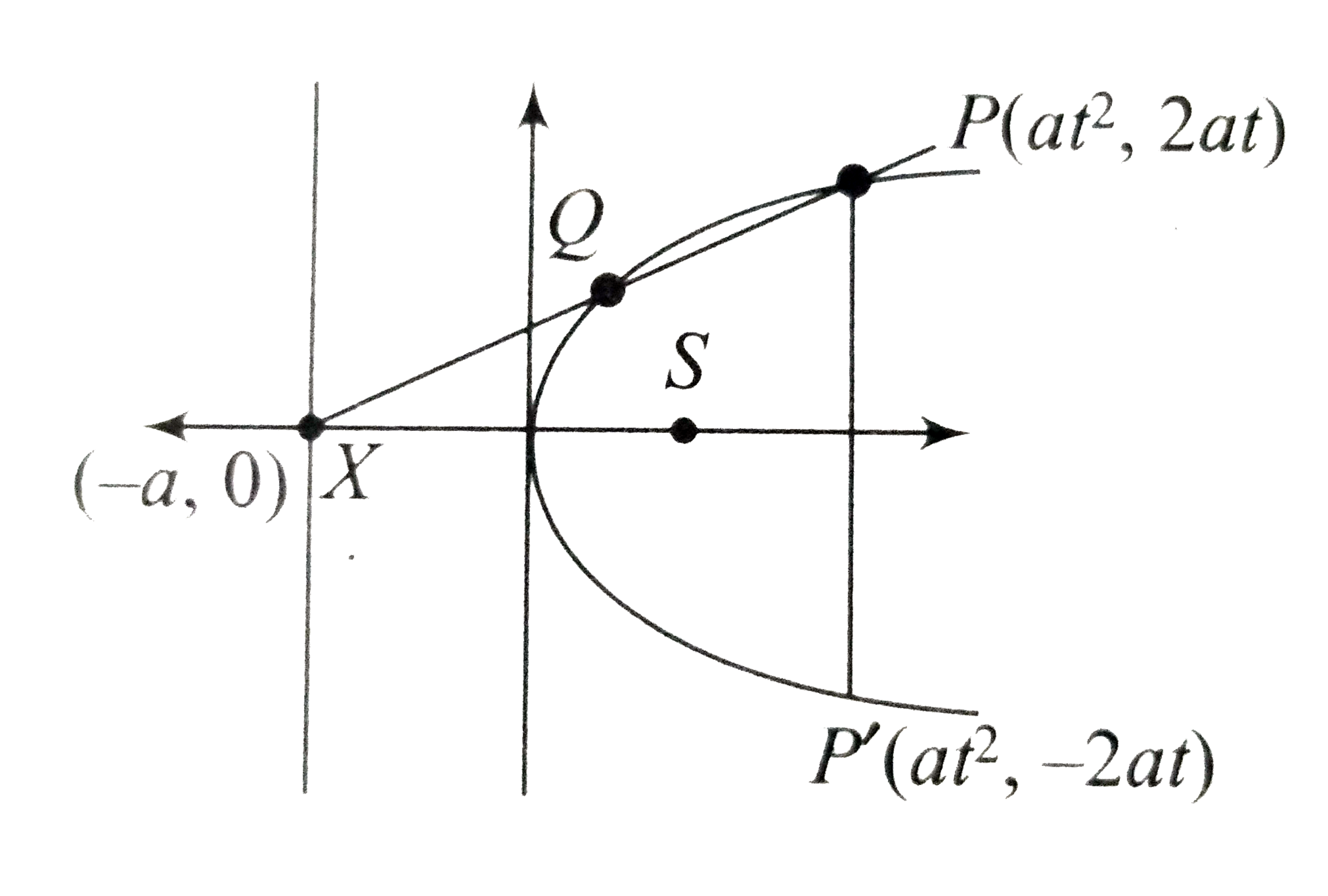
X:(−a,0)
PX:y=2at−0at2+a(x+a)
or (1+t2)y=2t(x+a)
Solving with parabola y2=4ax, we get
4t2(x+a)2(1+t2)2=4ax
or t2(x+a)2=ax(1+t2)2
or t2x2−(a+at4)x+at2=0
or xt2(x−at2)−a(x−at2)=0
or x=at2
∴Q:(at2,2at)
Thus P'(at2−2at) and Q(at2,2at), are extremities of focal chord.
So, tangents at P' and Q intersect on directrix.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Multiple Correct Answers Type10videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Comprehension Type2videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - JEE Advenced Single Answer Type18videos
PARABOLA
- BOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Question Bank19videos
PERMUTATION AND COMBINATION
Similar Questions
Knowledge Check
- Question 1 - Select One
The focus of the parabola y2=−4ax is :
A(2, a)B(-a, 0)C(0,2)D(0, -2) - Question 2 - Select One
If X is the foot of the directrix on axis of the parabola. PP' is a double ordinate of the curve and PX meets the curve again in Q. Then prove that P' Q passes through fixed point which is
AvertexBfocusCmidpoint of vertex and focusDnone of these - Question 3 - Select One
If normals at the ends of the double ordinate x = 4 of parabola y2=4x meet the curve again in P and P' respectively, then PP' =
A6B12C10Dnone of these
The triangle formed by the tangents to a parabola y2=4ax at the ends of the latus rectum and the double ordinate through the focus is
View SolutionTangent at P(2,8) on the curve y=x3 meets the curve again at Q. Find coordinates of Q.
View SolutionTangent at P(2,8) on the curve y=x3 meets the curve again at Q.
Find coordinates of Q.View SolutionTangent at (2,8) on the curve y=x3 meets the curve again at Q.Find the coordinates of Q.
View SolutionIf the parabola y2=4ax passes through the point (2,-3) then find the co-ordinates of the focus and the length of latus rectum.
View Solution

