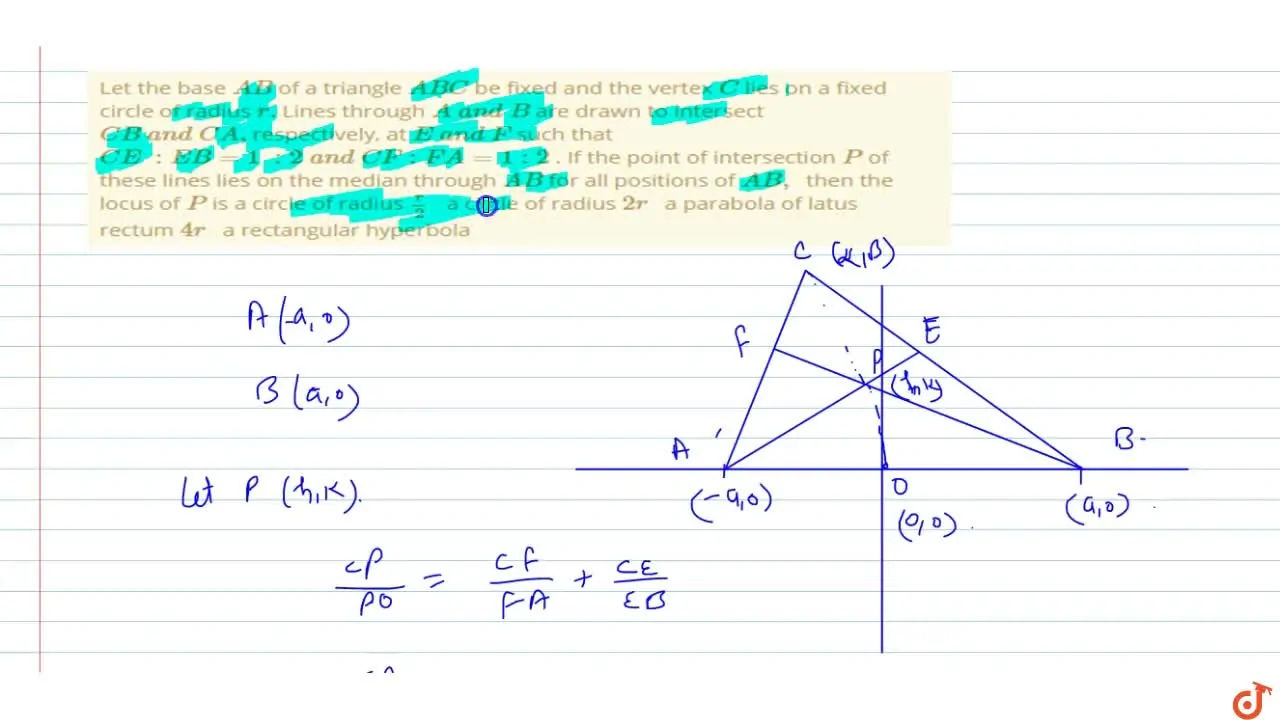
Let the base AB of a triangle ABC be fixed and the vertex C lies on a fixed circle of radius r. Lines through AandB are drawn to intersect CBandCA, respectively, at EandF such that CE:EB=1:2andCF:FA=1:2 . If the point of intersection P of these lines lies on the median through AB for all positions of AB, then the locus of P is a circle of radius r2 a circle of radius 2r a parabola of latus rectum 4r a rectangular hyperbola
Step by step video & image solution for Let the base A B of a triangle A B C be fixed and the vertex C lies on a fixed circle of radius rdot Lines through Aa n dB are drawn to intersect C Ba n dC A , respectively, at Ea n dF such that C E: E B=1:2a n dC F : F A=1:2 . If the point of intersection P of these lines lies on the median through A B for all positions of A B , then the locus of P is a circle of radius r/2 a circle of radius 2r a parabola of latus rectum 4r a rectangular hyperbola by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
In figure, ABE is a in which AE=BE . Circle passing through A and B intersects AE and BE at D and C respectively. Prove that DC∣∣AB.
View SolutionThe vertices of a ABC are A(5,5),B(1,5)andC(9,1) . A line is drawn to intersect side AB and AC at P and Q respectively, such that APAB=AQAC=34. Find the length of the line segment PQ.
View SolutionABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively intersecting at P, Q and R . Prove that the perimeter of PQR is double the perimeter of ABC
View SolutionIn a triangle ABC , let PandQ be points on ABandAC respectively such that PQ∣∣BC . Prove that the median AD bisects PQ.
View SolutionA variable plane passes through a fixed point (1,−2,3) and meets the coordinate axes at points A, B, C then the point of intersection of the planes through A, B, C parallel to the coordinate planes lies on:
View SolutionA variable plane passes through a fixed point (1,−2,3) and meets the coordinate axes at point A, B, C then the point of intersection of the planes through A, B, C parallel to the coordinate planes lies on
View SolutionABCD is a parallelogram and EandF are the centroids of triangles ABD and BCD respectively, then EF= (a)AE (b) BE (c) CE (d)DE
View SolutionA variable line intersects the co-ordinate axes at A and B and passes through a fixed point (a,b).then the locus of the vertex C of the rectangle OACB where O is the origin is
View SolutionD and E are, respectively, the points on equal sides AB and AC of an isosceles triangle ABC such that B, C, E, and D are concyclic as shown in Figure. If O is the point of intersection of CD and BE, prove that AO is the bisector of line segment DE
View SolutionABC is a triangle in which D is the mid-point of BC ,E andF are mid-points of DC and AE respectively. If area of ABC is 16cm2, find the area of DEF
View Solution