Log be defined for every real value of then the possible value of is 3 (b) 4 (c) 5 (d) 6Solution in Tamil
The correct Answer is:3
or [a should be less than the minimum value of and a must be greater than the maximum value of ]
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - JEE Previous Year12videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Matrix)9videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank28videos
Quadratic Equations, Inequalities, Modulus and Logarithms
- BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
Similar Questions
For real x, let f(x)=x3+5x+1 , then (1) f is oneone but not onto R (2) f is onto R but not oneone (3) f is oneone and onto R (4) f is neither oneone nor onto R
03:11View SolutionThe function f(x) is defined on the interval [0, 1]. Now, match the following lists:
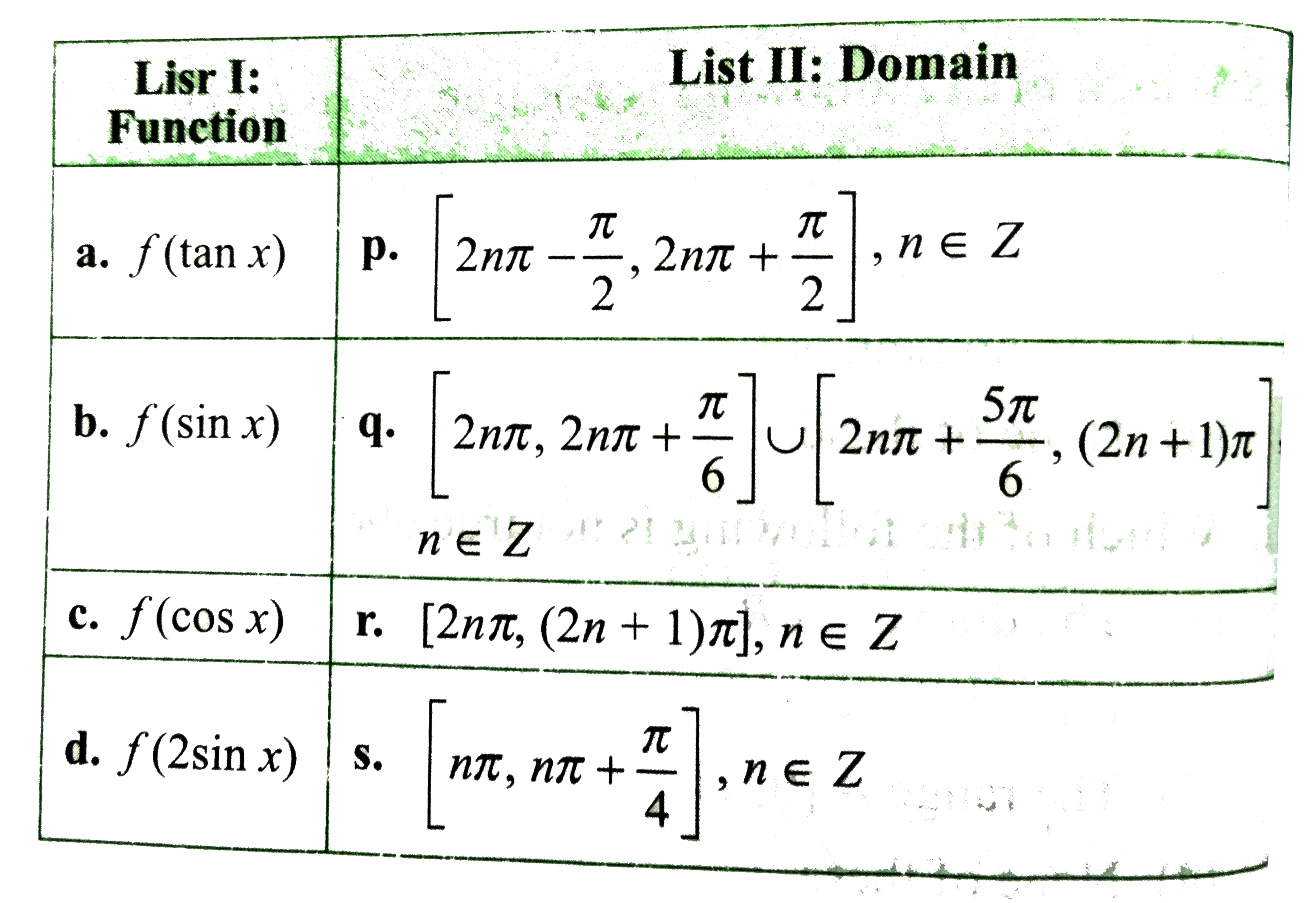 04:24View Solution
04:24View SolutionLet a,b,c,d be positive integers such that (log)ab=32and(log)cd=54. If (a−c)=9, then find the value of (b−d).
03:25View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj+ˆk and ˆi−ˆj+ˆk, in the order from right-handed system ∀x ∈R, is
08:53View SolutionLeg f(x)=log((log)1/3((log)13((log)7(sinx+a))) be defined for every real value of x, then the possible value of a is 3 (b) 4 (c) 5 (d) 6
03:20View Solution. If log2,log(2x-1) and log(2x+3) are in A.P.then the value of x is (A) 5/2(C)log,5 (B) log25(D)logs3
04:18View SolutionThe maximum integral values of x in the domain of f(x)=log10(log1/3(log4(x−5)) is :
03:24View SolutionIf range of f(x)=(lnx)(lnx2)+lnx3+3ln2x+lnx2+2 can be expressed as [ab,cd] where a,b,c and d are prime numbers (not nacessarily distinct) then find the value of (a+b+c+d)2.
03:01View SolutionLet f(x)=log(log)13((log)7(sinx+a))) be defined for every real value of x, then the possible value of a is 3 (b) 4 (c) 5 (d) 6
06:21View SolutionLet f(x)=log1/3((log)13((log)7(sinx+a)) be defined for every real value of x, then the possible value(s) of a is (a) 3 (b) 4 (c) 5 (d) 6
02:32View SolutionThe number of integral values of a for which f(x)=log((log)13((log)7(sinx+a))) is defined for every real value of x is ________
03:00View SolutionLet f(x)=log(log1/3(log7(sinx+a))) be defined for every real value of x, then the possible value of a is
03:11View SolutionIf range of f(x)=(lnx)(lnx2)+lnx3+3ln2x+lnx2+2 can be expressed as [ab,cd] where a,b,c and d are prime numbers (not nacessarily distinct) then find the value of (a+b+c+d)2.
04:18View SolutionThe maximum integral values of x in the domain of f(x)=log10(log1/3(log4(x−5)) is : (a). 5 (b). 7 (c). 8 (d). 9
02:38View SolutionThe value of ∫e6logx−e5logxe4logx−e3logxdx is equal to
03:06View SolutionThe value ∫{ln(1+sinx)+xtan(π4−x2)}dx is equal to (A) xln(1+sinx)+C (B) ln(1+sinx)+C (C) −xln(1+sinx)+C (D) ln(1−sinx)+C
02:12View Solution

