Major and Minor Arc
Step by step video & image solution for Major and Minor Arc by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Similar Questions
Major and minor grooves occurs in
View SolutionMajor and Minor segment
View SolutionDiscussion OF exercise-12.1 || area OF ring || Major and minor segment || Area OF major and minor sector || Area OF major and minor segment || Arc || Arc length OF major and minor segment
View Solution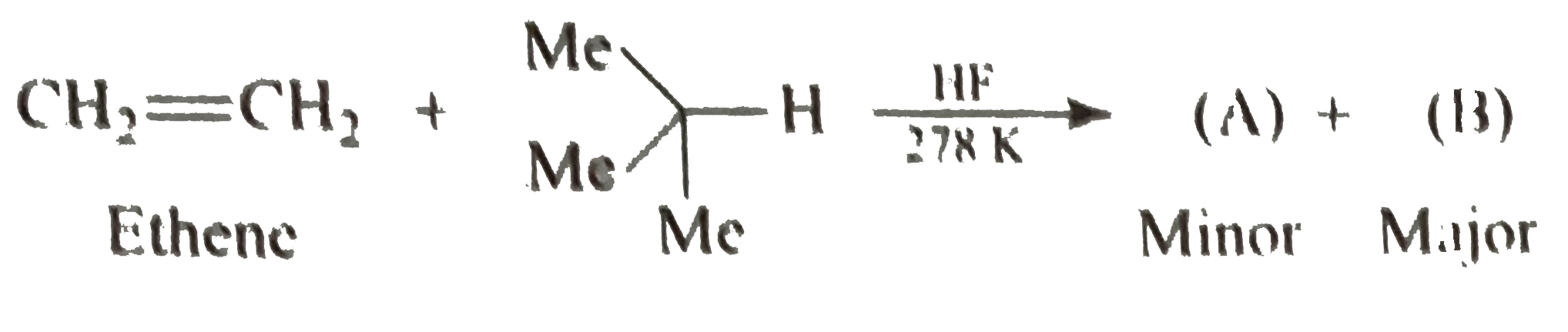
Give the major and minor products.View SolutionGive the major and minor porducts.
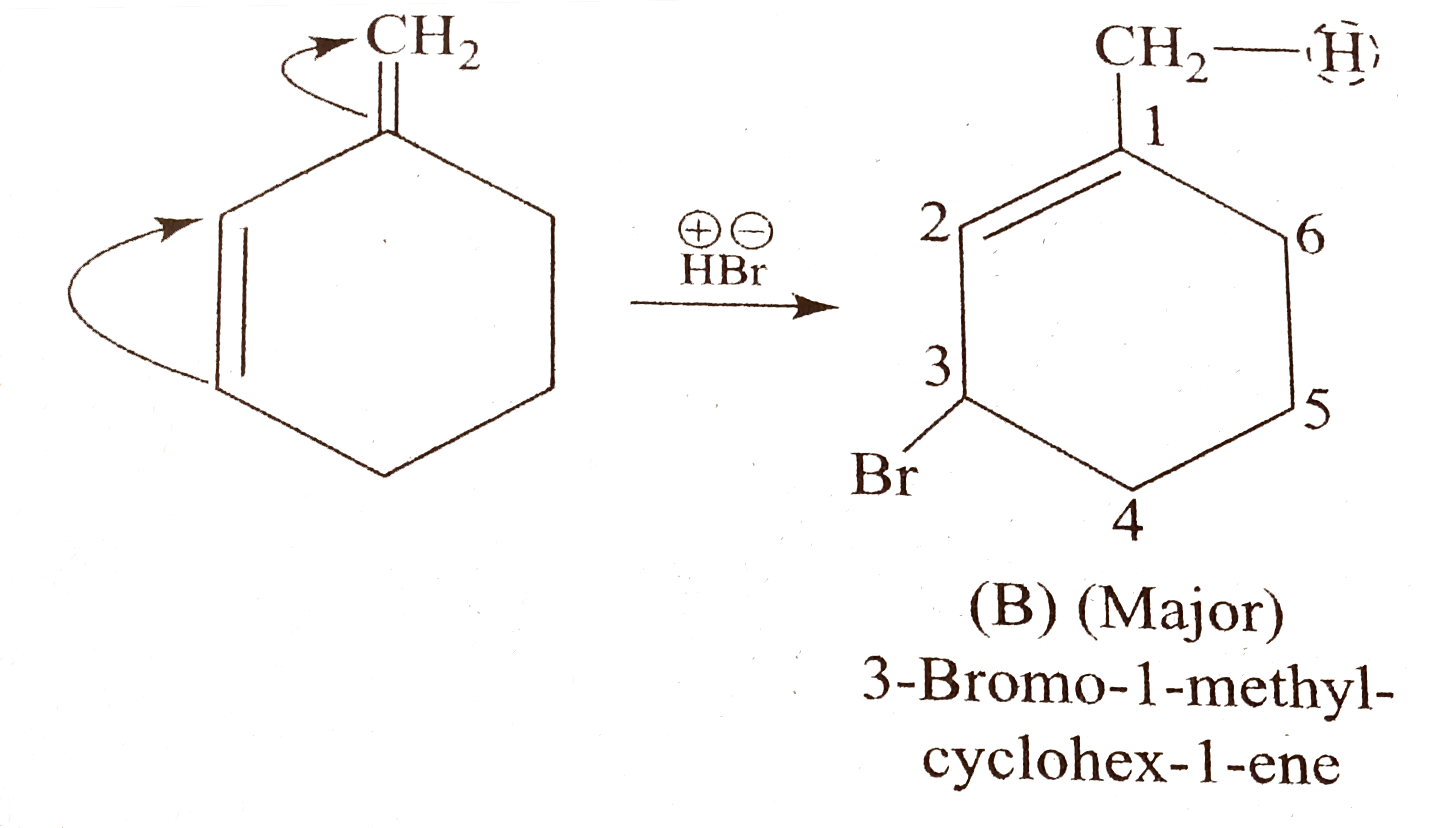 View Solution
View SolutionIdentify the major and minor products in the following reactions
 View Solution
View SolutionWhere can we find major and minor grooves ?
View SolutionIdentify the major and minor products in the following reactions
 View Solution
View SolutionGive the major and minor products of the dehydration of the given compound.
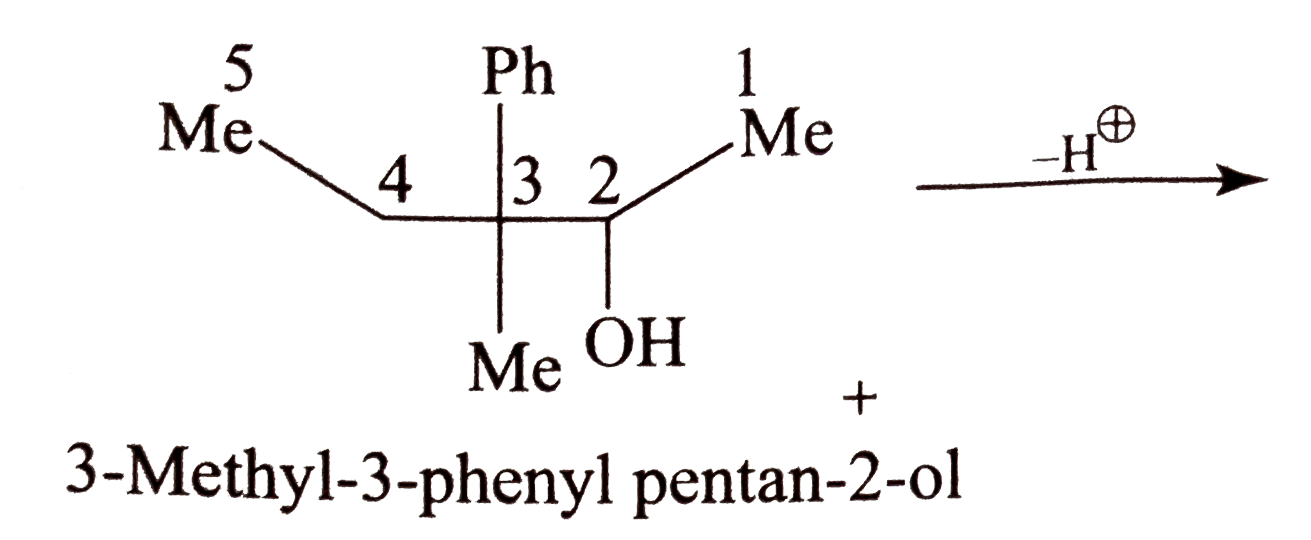 View Solution
View SolutionComplete the following:
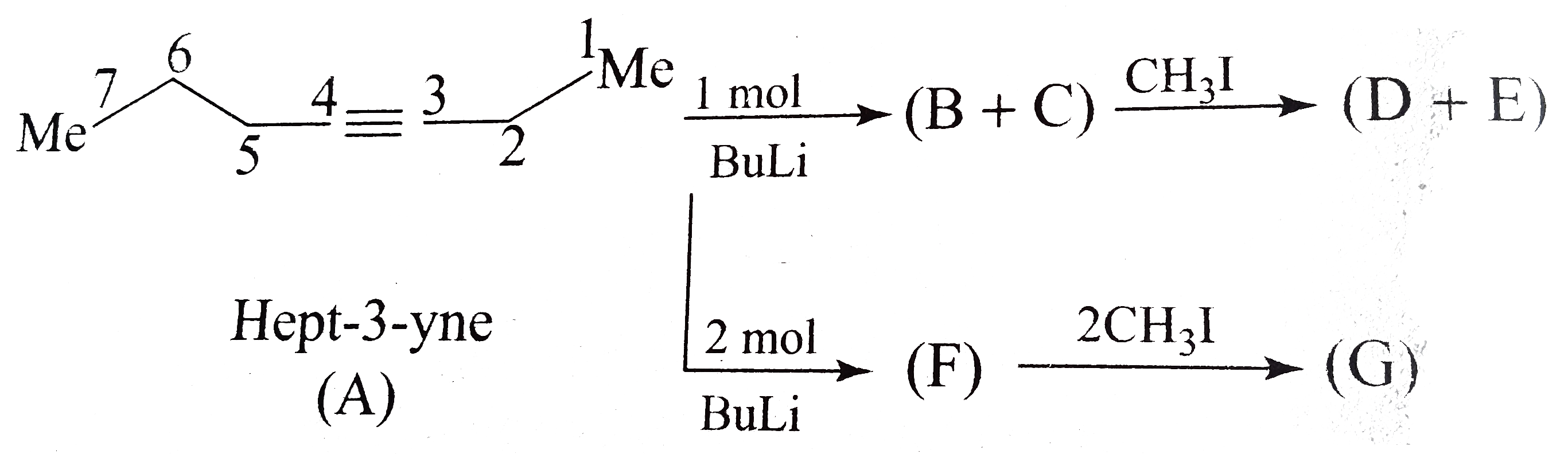
Give the major and minor products (C and D).View Solution


