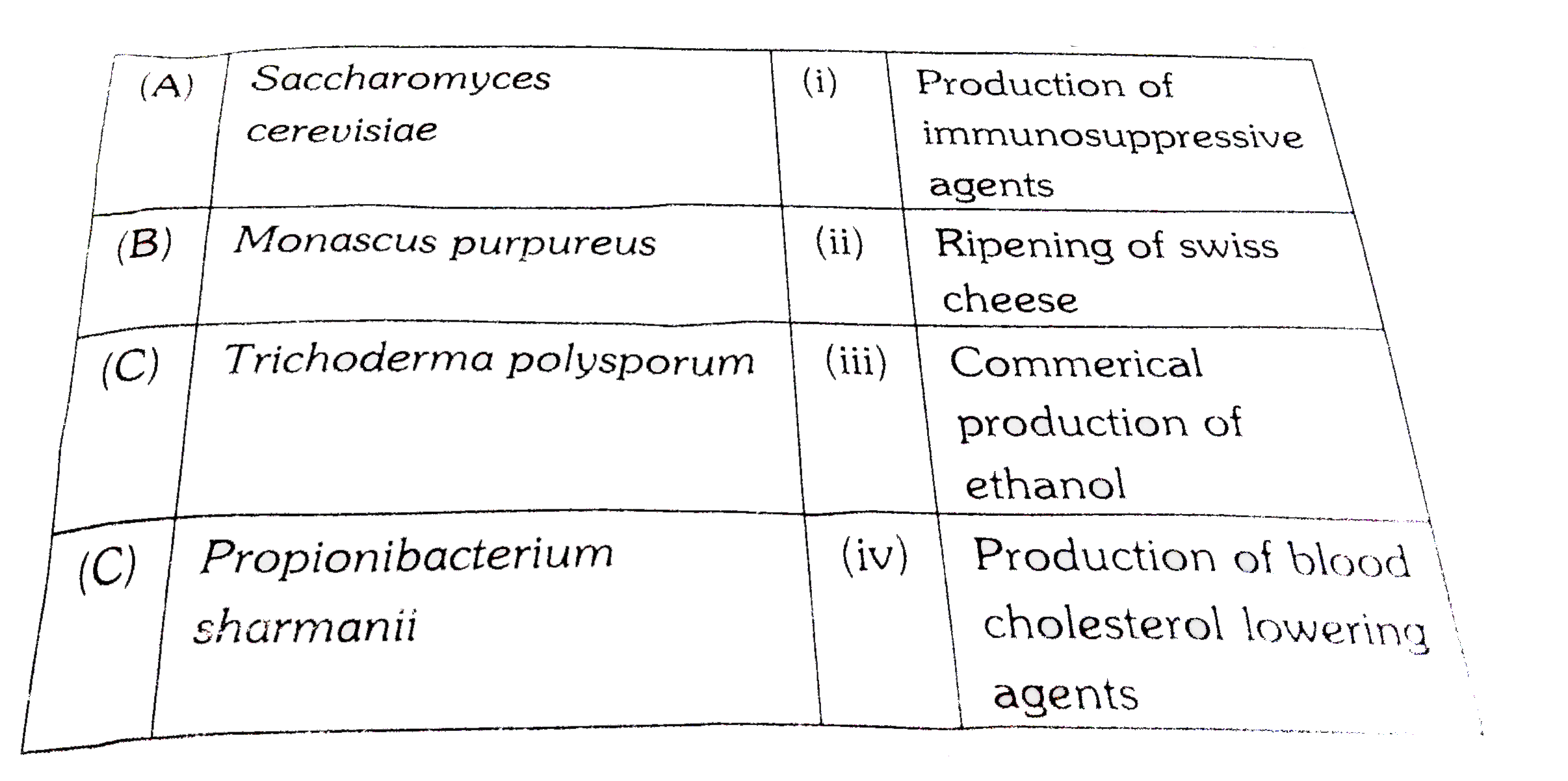Match the following lists:

a→p,b→q,r,c→s,r,d→q,r.
a. f(1−x)=f(1+x)
∴ −f'(1−x)=f'(1+x)
Hence, graph of f(x) is symmetrical about point (1, 0) [ as if f(x) = - f(-x), then f(x) is odd and its graphs is symmetrical about (0,0). Now shift the graph at (1,0)].
b. f(2−x)+f(x)=0
Replacexby1+x.Thenf(2−(1+x))+f(1+x)=0
or f(1−x)+f(1+x)=0
or −f'(1−x)+f'(1+x)=0
or f'(1−x)=f'(1+x) (1)
Therefore, graph of f'(x) is symmetrical about line x=1.
Alos, put x=2 in (1). Then f'(-1)=f'(3).
c. f(x+2)+f(x)=0 (1)
Replace xbyx+2.thenf(x+4)+g(c+2)=0 (2)
From (1) and (2), we have f(x) = f(x+4)
Hence, f(x) is periodic with period 4.
Also, f'(x)=f'(x+4).
Hence, f'(x) is periodic with period 4.
Put =−1∈f'(x)=f'(x+4).Thenf'(−1)=f'(3).
d. Putting x=0,y=0,we≥t2f(0)+{f(0)}2=1
or f(0)=√2−1 [∵f(0)>0]
Putting y=x,2f(x)+{f(x)}2=1
Differentiating w.r.t. x, we get
2f'(x)+2f⋅f'(x)=0
or f'(x){1+f(x)}=0
or f'(x)=0, because f(x)>0.
Topper's Solved these Questions
- DIFFERENTIATIONBOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIATIONEXERCISE - Numerical Value Type
45 Videos
- DIFFERENTIATIONBOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIATIONEXERCISE - Archives
14 Videos
- DIFFERENTIATIONBOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIATIONEXERCISE - Linked Comprehension Type
24 Videos
- DIFFERENTIAL EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Matrix Match Type
5 Videos
- DOT PRODUCTBOOK - CENGAGE ENGLISHCHAPTER - DOT PRODUCTEXERCISE - DPP 2.1
15 Videos
Similar Questions
Knowledge Check
Match the following list of bacteria and their commercially important products.
BacteriumProduct(i)Aspergillus niger(A)Lactic acid(ii)Acetobacter aceti(B)Butyric acid(iii)Clostridium butylicum(C)Acetic acid(iv)Lactobacillus(D)Citric acid
Choose the correct match.Ai−(B),ii−(C),iii−(D),iv−(A)Bi−(B),ii−(D),iii−(C),iv−(A)Ci−(D),ii−(C),iii−(B),iv−(A)Di−(D),ii−(A),iii−(C),−iv−(B)
Match the following list of bacteria and their commercially important products
Choose the correct match

View SolutionMatch the following list of bioactive sub- stances and their roles
Choose the correct match

View SolutionMatch the following list of animals with their level of organisation.
Choose the correct match sryowing division of labour with animal example.

View SolutionMatch the following list of animals with their level of organisation :
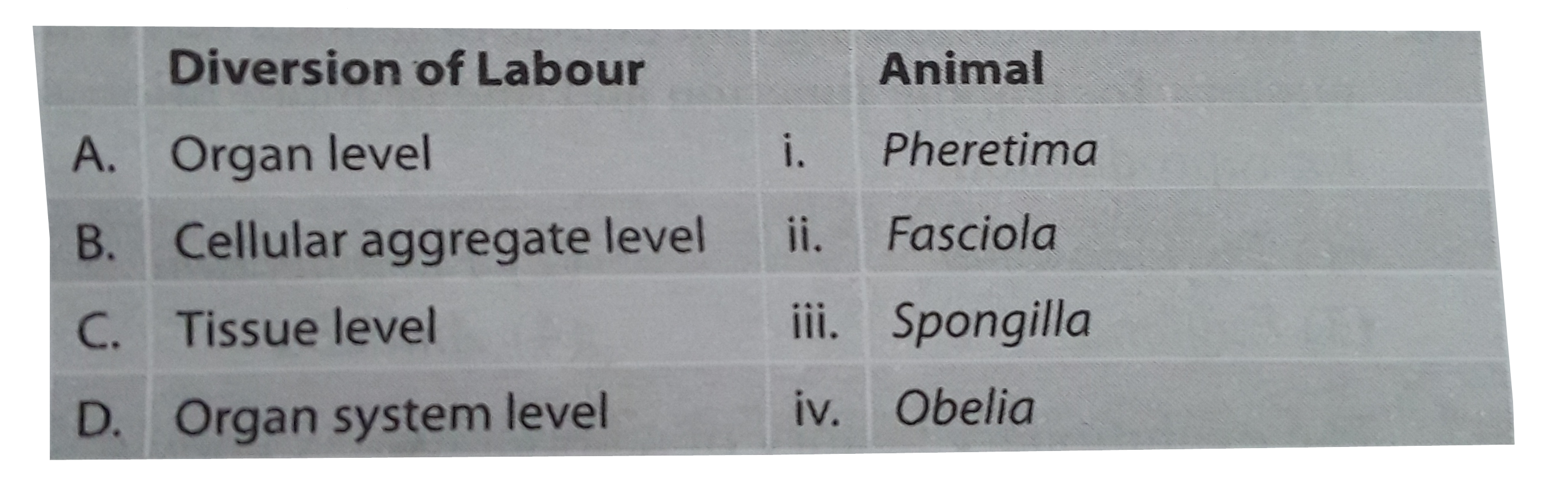
Choose the correct match showing division of labour with animals.
View SolutionMatch the following list of bacteria and their commercially important products.
BacteriumProduct(i)Aspergillus niger(A)Lactic acid(ii)Acetobacter aceti(B)Butyric acid(iii)Clostridium butylicum(C)Acetic acid(iv)Lactobacillus(D)Citric acid
Choose the correct match.
View SolutionMatch the following list of animals with their level of organisation.
Division of LabourAnimalA.Organ leveli.PheretimaB.Cellular aggregate levelii.FasciolaC.Tissue leveliii.SpongillaD.Organ system leveliv.Obelia
Choose the correct match showing division of labour with animal example.
View SolutionMatch the following list of bioactive substances and their roles.
Bioactive substanceRole(i)Statin(A)Removal of oil stains(ii)CyclosporinA(B)Removal of clots from blood vessels(iii)Streptokinase(C)Lowering of blood cholesterol(iv)Lipase(D)Immuno-suppressive agent
Choose the correct match.
View Solution