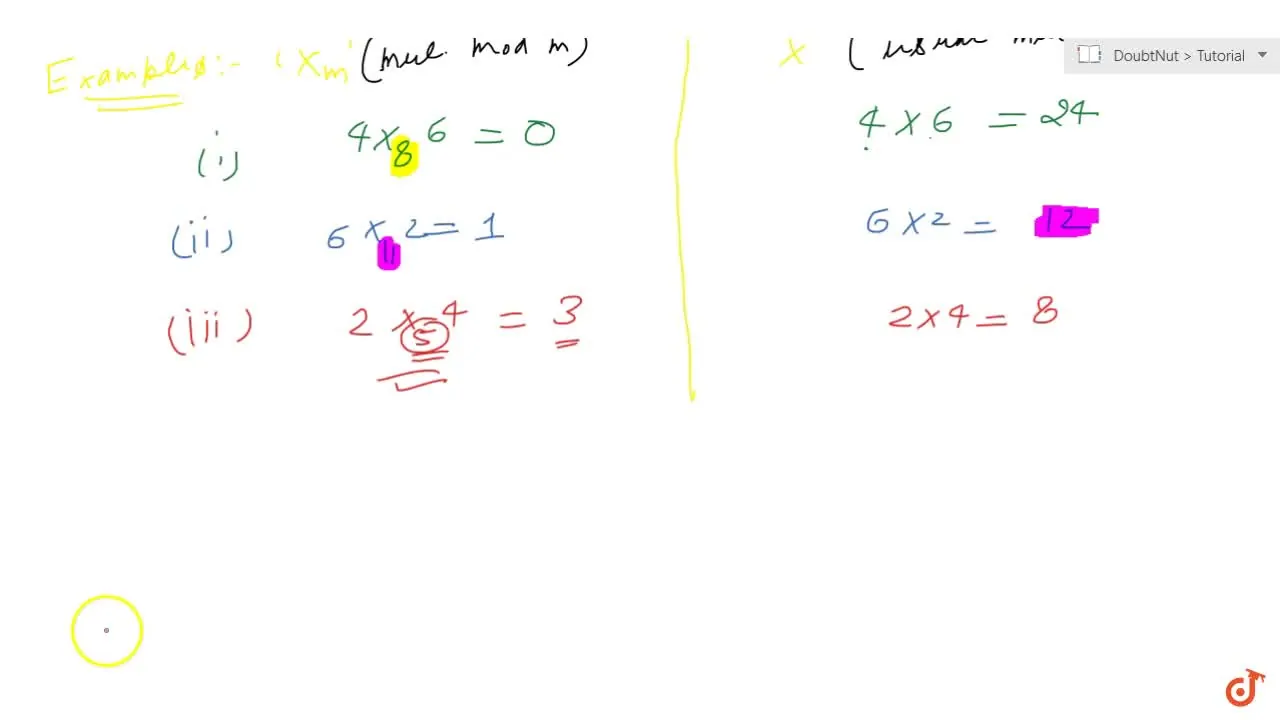Multiplication modulo
What is Multiplication modulo?
Let's explore the addition property of modular arithmetic:
(A + B) mod C = (A mod C + B mod C) mod C
Example:
Let A=14, B=17, C=5
Let's verify: (A + B) mod C = (A mod C + B mod C) mod C
LHS = Left Hand Side of the Equation
RHS = Right Hand Side of the Equation
LHS = (A + B) mod C
LHS = (14 + 17) mod 5
LHS = 31 mod 5
LHS = 1
RHS = (A mod C + B mod C) mod C
RHS = (14 mod 5 + 17 mod 5) mod 5
RHS = (4 + 2) mod 5
RHS = 1
LHS = RHS = 1
Intuition Behind Modular Addition
Observe the figure below. If we want to calculate 12+9 mod 7 we can easily go around the modular circle for a sequence of 12+9 steps clockwise (as shown in the bottom left circle).
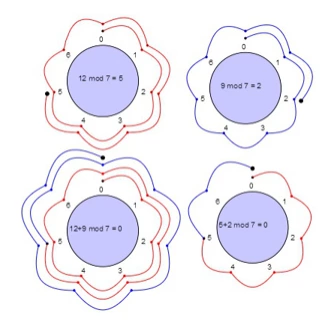
We can take a shortcut by observing that every 7 steps we end up in the same position on the modular circle. These complete loops around the modular circle don’t contribute to our final position. We ignore these complete loops around the circle by calculating each number mod 7 (as shown in the two upper modular circles). This will give us the number of clockwise steps, relative to 0, that contributed to each of their final positions around the modular circle.
Now, we only have to go around the circle clockwise the total of the number of steps that contributed to each of numbers final position (as shown in the bottom right modular circle). This method applies, in general, to any two integers and any modular circle.
Proof for Modular Addition
We will prove that (A + B) mod C = (A mod C + B mod C) mod C
We must show that LHS=RHS
From the quotient remainder theorem we can write A and B as:
A = C * Q1 + R1 where 0 ≤ R1 < C and Q1 is some integer. A mod C = R1
B = C * Q2 + R2 where 0 ≤ R2 < C and Q2 is some integer. B mod C = R2
(A + B) = C * (Q1 + Q2) + R1+R2
LHS = (A + B) mod C
LHS = (C * (Q1 + Q2) + R1+ R2) mod C
We can eliminate the multiples of C when we take the mod C
LHS = (R1 + R2) mod C
RHS = (A mod C + B mod C) mod C
RHS = (R1 + R2) mod C
LHS=RHS= (R1 + R2) mod C
Modular Subtraction
A very similar proof holds for modular subtraction
(A - B) mod C = (A mod C - B mod C) mod C
Let’s have a look at an example
A + B) = C * (Q1 + Q2) + R1+R2
(1)LHS = (A + B) mod C
(2)LHS = (C * (Q1 + Q2) + R1+ R2) mod C
We can eliminate the multiples of C when we take the mod C
LHS = (R1 + R2) mod C
WHAT DOES (3) MEAN BY DETAIL?
Solution
Here's what it means:
If we are calculating X mod C, then:
we can add multiples of C to X or subtract multiples of C from X and the result mod C will not change
i.e. X mod C = (X+ K * C) mod C where K is an integer
e.g. 5 mod 7 = ( 5 + 7 )mod 7 = (5 + 2 * 7) mod 7 = (5 - 29 * 7) mod 7 = (5 + 42 * 7) mod 7 = 5
This is discussed in previous articles
The contribution of the multiple of C mod 7 is 0.
Why is this true?
From the quotient remainder theorem we have:
X = Q * C + R , where 0 <= R < C
Let's add an integer multiple of C to both sides of this equation
i.e. let's add K * C where K is some integer
X + K * C = Q * C + R + K * C
Now we group the terms on the right hand side
X + K * C = (Q + K) * C + R
The result of adding integers Q + K is just another integer
Let's call this new integer G
The result of X + K * C is just another integer
Let's call this new integer Y
Y = G * C + R, where 0 <= R < C
This is the exact form of the quotient remainder theorem!!
Thus the remainder of Y divided by C is R
But Y = X + K * C
So the remainder of X + K * C divided by C is R.
But this means than X and X + K * C have the same remainder R.
So in the specific example
(R1 + R2) mod C = (C * (Q1 + Q2) + R1+ R2) mod C
because this is in the form
X mod C = (X+ K * C) mod C
LHS = Left Hand Side of the Equation
RHS = Right Hand Side of the Equation
LHS = (14 + 17) mod 5
LHS = 31 mod 5
LHS = 1
RHS = (14 mod 5 + 17 mod 5) mod 5
RHS = (4 + 2) mod 5
RHS = 1

We must show that LHS=RHS
B = C * Q2 + R2 where 0 ≤ R2 < C and Q2 is some integer. B mod C = R2
(A + B) = C * (Q1 + Q2) + R1+R2
LHS = (C * (Q1 + Q2) + R1+ R2) mod C
We can eliminate the multiples of C when we take the mod C
LHS = (R1 + R2) mod C
RHS = (R1 + R2) mod C
(1)LHS = (A + B) mod C
(2)LHS = (C * (Q1 + Q2) + R1+ R2) mod C
We can eliminate the multiples of C when we take the mod C
LHS = (R1 + R2) mod C
WHAT DOES (3) MEAN BY DETAIL?
If we are calculating X mod C, then:
we can add multiples of C to X or subtract multiples of C from X and the result mod C will not change
i.e. X mod C = (X+ K * C) mod C where K is an integer
e.g. 5 mod 7 = ( 5 + 7 )mod 7 = (5 + 2 * 7) mod 7 = (5 - 29 * 7) mod 7 = (5 + 42 * 7) mod 7 = 5
This is discussed in previous articles
The contribution of the multiple of C mod 7 is 0.
From the quotient remainder theorem we have:
X = Q * C + R , where 0 <= R < C
Let's add an integer multiple of C to both sides of this equation
i.e. let's add K * C where K is some integer
X + K * C = Q * C + R + K * C
X + K * C = (Q + K) * C + R
The result of adding integers Q + K is just another integer
Let's call this new integer G
The result of X + K * C is just another integer
Let's call this new integer Y
This is the exact form of the quotient remainder theorem!!
Thus the remainder of Y divided by C is R
But Y = X + K * C
But this means than X and X + K * C have the same remainder R.
So in the specific example
(R1 + R2) mod C = (C * (Q1 + Q2) + R1+ R2) mod C
because this is in the form
X mod C = (X+ K * C) mod C
Similar Questions
Multiple
View Solutionalgebra OF matrix- addition || scalar multiplication || multiplication OF 2 matrix || properties OF multiplication
View SolutionMultiplication of literals
View SolutionMultiplication OF determinants
View SolutionMultiplication of Matrices
View SolutionAddition Modulo
View SolutionWrite the multiplication table for the set of integers modulo 5.
View SolutionMultiplication Of Integers|Properties Of Multiplication Of Integers|Closure Property|Commutative Property|Multiplication By Zero|Multiplicative Identity|Multiplicative Inverse Of An Integer|Problem Practice|OMR
View SolutionLet A={1,-1,I,-i} hbe the set of four 4th roots of unity prepare the commposition table for multiplication on A and show that ltrbgt (i) A is closed for multiplication
(ii) multiplication is associative on A
(iii) multiplication is commutative on A
(iv) 1 is the multiplicative identity
(v) every element in A has its multiplicative iverseView SolutionDistributivity of multiplication over addition the multiplication of rational numbers is distributive over their addiction.
View Solution