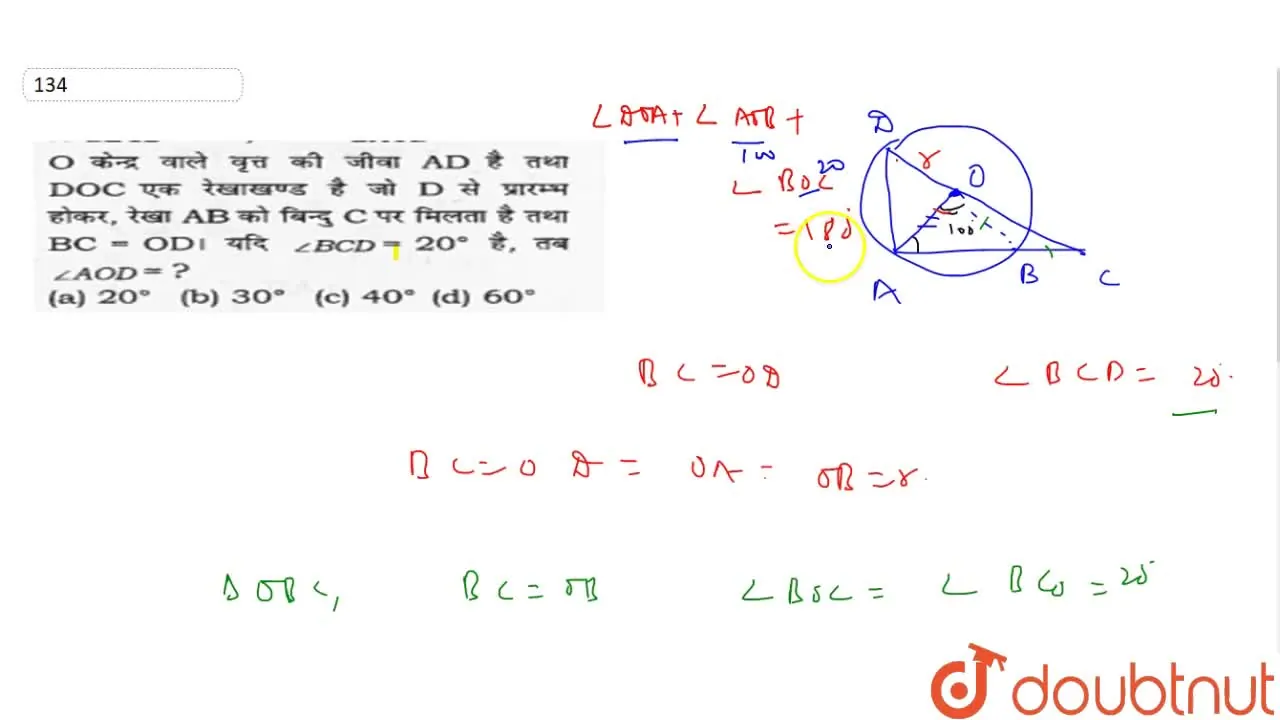
O केंद्र वाले वृत्त की जीवा AD हे तथा DOC क रेखाखण्ड हे जो D से प्र्रारंब होकर, रेखा AB को बिंदु C पर मिलता हे, तथा BC=OD यदि ∠BCD=20∘ हे, तब ∠AOD=?
20∘
30∘
40∘
60∘
The correct Answer is:D
According to equation,

BC=DO=OA=OB=r
In ΔOBC
∠OCB=∠COB=20∘
In ΔAOB
∠OBA=20∘+20∘
∠OBA=40∘
∠OBA=∠OAB=402
InΔOAB=∠OAB=40∘
In ΔAOB
∠A+∠O+∠B=180∘
40∘+∠O+40∘=180∘
∠O=100∘
DOC is a line
∠COB+∠AOB+∠DOA=180∘
∠DOA=60∘
Related Playlists
Similar Questions
1,00,000 की राशि पर दो तरह के बट्टे, जिसमे एक बट्टा 40% है और दूसरा बट्टा दो क्रमवार 36% तथा 4% है दोनों तरह के बट्टे में कितना अंतर है
01:51View Solutionज़मींन पर किसी बिंदु से एक विमान उन्नतांश 45∘ है । 15 सेकेण्ड उड़ने के बाद उन्नतांश घटकर 30∘ हो जाता है । यदि विमान 2500 मीटर की ऊंचाई पर उड़ रहा है , तो विमान की गति कितने की . मि. /घंटा है ?
02:37View SolutionΔFGH एक समद्विबाहु त्रिभुज हे, तथा FG<3 cm, GH=8cm हे, तब सही कथन ज्ञात करे?
03:01View Solutionतीन असंरेखीये बिंदु A ,B तथा C से होकर जाने वाले वृत्त के केंद्र का बिन्दुपथ निर्धारित कीजिये।
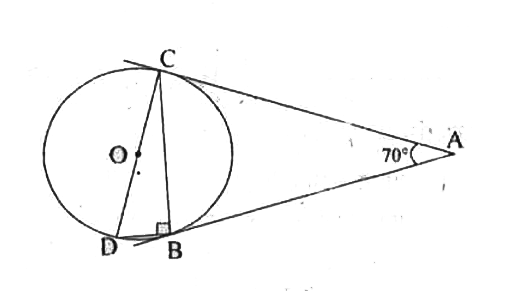
02:52View Solutionदी गई आकृति में बिंदु B ,C तथा D से गुजरने वाले वृत्त के बिंदु B तथा C पर AB तथा AC स्पर्श रेखाएं है। यदि ∠BAC=70∘ और ∠CBD=90∘ तो ∠BCD का मान है -
 03:41View Solution
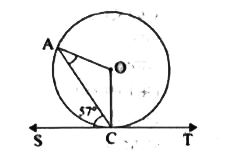
03:41View Solutionदी गई आकृति में O वृत्त का केंद्र तथा SCT बिंदु C पर स्पर्श रेखा है। यदि ∠ACS=57∘ हो ,तो ∠OAC की माप है -
 05:41View Solution
05:41View Solution8.8cm लम्बा एक रेखाखण्ड AB खींचिए। A को केंद्र मानकर 4 त्रिज्या का एक वृत्त तथा 3 को केंद्र लेकर त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केंद्र से स्पर्श रतेखाओ कि रचना कीजिए।
06:20View Solutionवह समतल, जो बिन्दुओ (−3,−3,4) तथा (3,7,6) को मिलाने वाले रेखाखण्ड का लंबसमद्विभाजक करता है, निम्न में से किस एक बिंदु से होकर जाता है?
06:39View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
04:47View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
03:00View SolutionAB is the chord of a circle with centre O and DOC is a line segment originating from a point D on the circle and intersecting AB produced at C such that BC = OD. If ∠BCD=20∘, then ∠AOD= ?
37:29View Solutionयदि एक प्रिज्म के लाल , पीले और बैगनी रंगो के लिए अपवर्तनांक क्रमशः 1.61, 1.63 तथा 1.65 है , तो प्रिज्म की विक्षेपण क्षमता है
02:03View Solutionवृत्त|जीवा द्वारा किसी बिंदु पर आन्तरित कोण#!#केंद्र से जीवा पर लम्ब#!#महत्वपूर्ण प्रश्न
View SolutionIf radius of a circle is increased by 5%, then the increase in its area is? यदि किसी वृत्त की त्रिज्या 5% बढ जाती है, तो इसके क्षेत्रफल में कितने प्रतिशत की वृद्धि हो जाती हे?
05:20View Solutionहे भूख / मत मचल प्यास, तड़प मत हे नींद / मत सता क्रोध, भया उथल-पुथल हे मोह पाश अपने ढील लोभ, मत ललचा हे मद / मत कर मदहोश ईया, जला मत ओ घराचर / मत एक अवसर आई हूँ संदेश लेकर चन्नमल्लिकार्जुन का प्रस्तुत काव्यांश में चन्नमल्लिकार्जुन से क्या अभिप्राय है?
03:33View Solution