O is any point on the diagonal PR of a parallelogram PQRS (figure). Prove that ar(ΔPSO)=ar(ΔPQO).

Given In a parallelogram PQRS, O is any point on the diagonal PR.
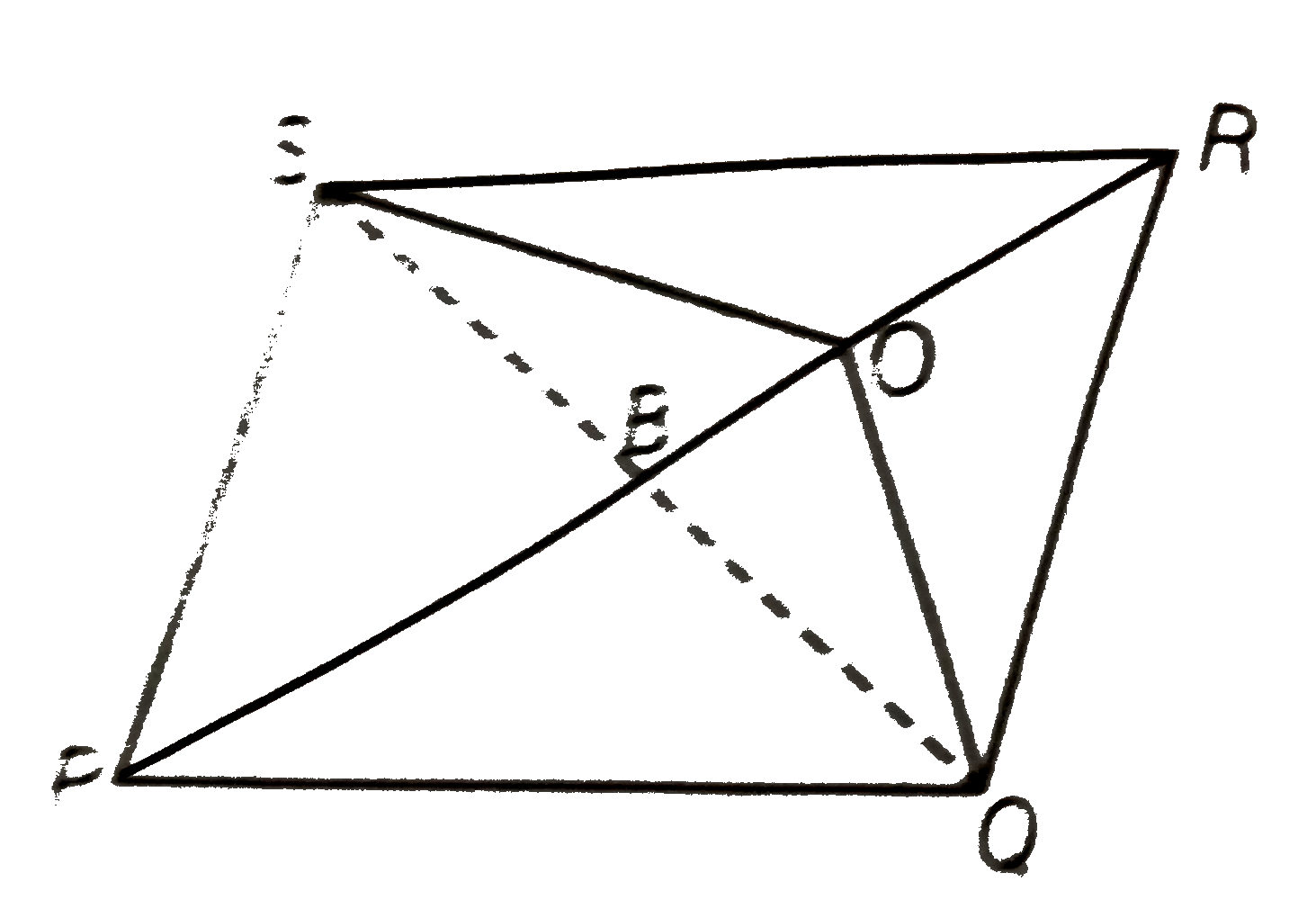
To prove ar(ΔPSO)=ar(ΔPQO)
Construction Join SQ which intersects PR at B.
Proof We know that, diagonals of a parallelogram bisect each other, so B is the mid-point of SQ.
Here, PB is a median of ΔQPS and we know that, a median of a triangle divides it into two triangles of equal area.
∴ ar(ΔBPQ)=ar(ΔBPS) ...(i)
Also, OB is the median of ΔOSQ.
∴ ar(ΔOBQ)=ar(ΔOBS) ...(ii)
On adding Eqs. (i) and (ii), we get
ar(ΔBPQ)+ar(ΔOBQ)=ar(ΔBPS)+ar(ΔOBS)
⇒ ar(ΔPQO)=ar(ΔPSO) Hence proved.
Topper's Solved these Questions
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions
10 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.2 Very Short Answer Type Questions
5 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.4
14 Videos
Similar Questions
O' is any point on diagonal AC of a parallelogram ABCD. Prove that :
area of ΔAOD= area of ΔAOB
View SolutionO is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△OAB)=ar(△OBC)
View SolutionO is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△OAB)=ar(△OBC)
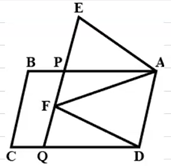
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
View SolutionProve that the diagonals of a parallelogram bisect each other.
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP.
View SolutionIn the given figure, AP||BQ||CR. Prove that ar(ΔAQC)=ar(ΔPBR)

View SolutionM and N are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CN is parallel to AM.
View SolutionTwo points X and Y lie on the diagonal BD of a parallelogram ABCD such that DX = BY. Prove that □AXCY is a parallelogram.
View SolutionIf the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle. Prove it.
View Solution
