समाकलन द्वारा धनात्मक x - अक्ष तथा (1,√3) पर वृत्त x2+y2=4 से स्पर्श रेखा तथा अभिलम्ब से बने त्रिभुज का क्षेत्रफल ज्ञात कीजिये |
दिया है : वृत्त का समीकरण
x2+y2=4 ... ( 1)
समीकरण (1 ) से बिंदु P पर स्पर्श रेखा का समीकरण
x⋅1+y√3=4 ... (2 )
यह A(4,0) पर x - अक्ष (y=0) पर मिलते है |
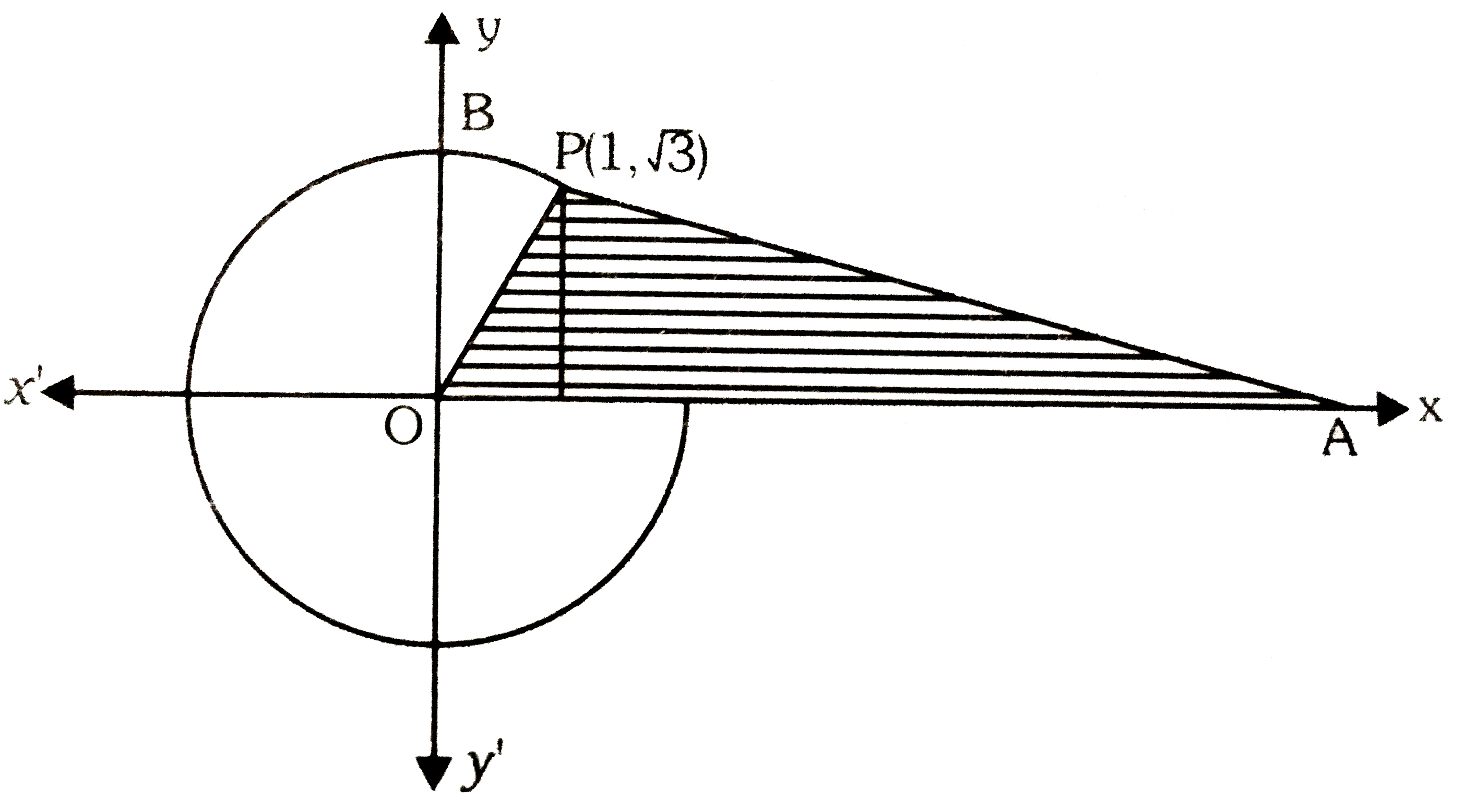
बिंदु P पर अभिलम्ब
y−√3=√3(x−1)[∵ समीकरण (2 ) की ढाल −1√3]
⇒y=√3x ... (3)
अतः ΔOAP का अभीष्ट क्षेत्रफल
=∫10√3xdx+∫411√3(4−x)dx
=√3[x22]10+1√3[4x−x22]41
=√3[12−0]+1√3[(4×4−422)−(4−12)]
=√32+1√3(8−72)=√32+92√3
=2√3 वर्ग इकाई
Related Playlists
- BOOK - BALAJI PUBLICATIONCHAPTER - समाकलन के सरल अनुप्रयोग EXERCISE - अभ्यास प्रश्न 17.112videos
समाकलन के सरल अनुप्रयोग
- BOOK - BALAJI PUBLICATIONCHAPTER - समाकलन के सरल अनुप्रयोग EXERCISE - अभ्यास प्रश्न 17.29videos
समाकलन के सरल अनुप्रयोग
- BOOK - BALAJI PUBLICATIONCHAPTER - समाकलन EXERCISE - स्वमूल्यांकन परीक्षण24videos
समाकलन
- BOOK - BALAJI PUBLICATIONCHAPTER - समाकलन क्रमशः EXERCISE - स्वमूल्यांकन परीक्षण20videos
समाकलन क्रमशः
Similar Questions
y=ex,x=0 से x=a तक
04:18View Solutionपरवलय y2=4ax तथा रेखा y=2x द्वारा घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिये |
View Solutionमान ज्ञात कीजिए -∫(4e3x+1)dx
03:16View Solution1x2−9
04:07View Solutionवक्र y=logx,x−अक्ष,x=1/2तथाx=3/2 से घिरे भाग का क्षेत्रफल ज्ञात कीजिए।
02:11View Solutionवक्रो y=√5−x2तथा y = | x - 1 | से सीमाबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिये |
03:53View Solutionसरल रेखा 3x−√3y+1=0 द्वारा Y- अक्ष पर काटा गया अन्तः खण्ड तथा X-अक्ष के साथ बने कोण को ज्ञात कीजिए ।
04:20View Solutionकिसी रेखा पर मूलबिंदु से खींचा गया लम्ब x-अक्ष के साथ 60∘ का कोण बनाता है। रेखा अक्षों के साथ ऐसा त्रिभुज बनाती है जिसका क्षेत्रफल 54√3 वर्ग मात्रक है । रेखा का समीकरण ज्ञात कीजिए ।
02:56View SolutionY - अक्ष से 2 इकाई का अन्तः खण्ड काटने वाली तथा X-अक्ष कि धनात्मक दिशा सेtan−1(54) का कोण बनाने वाली रेखा का समीकरण ज्ञात कीजिए ।
02:36View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिंदु(1,2) से होकर जाती है जिसके द्वारा अक्षो से बने त्रिभुज का क्षेत्रफल 92 वर्ग इकाई है
04:43View Solutionपरवलय y=4−x2 तथा x -अक्ष से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए ।
04:11View Solutionसरल रेखा y=2x,X− अक्ष तथा कोटियों x=0 और x=3 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए ।
08:25View Solutionउस रसाल रेखा का समीकरण ज्ञात कीजिए जो अक्षो पर समान अन्तः खण्ड काटे तथा रेखा अक्षो से घिरे त्रिभुज का क्षेत्रफल 8 वर्ग मात्रक हो।
04:24View Solutionवृत्त x2+y2=a2 तथा वक्र y=|x| से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
02:59View Solutiony = |x|, x= - 3, x = 1 व x-अक्ष से परिबध्द क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
06:54View Solutionवृत्त x2+y2=16 तथा परवलय x2=6y से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
06:22View Solution


