Prove that angle in the same segment of a circle are equal.
Step by step video & image solution for Prove that angle in the same segment of a circle are equal. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Prove that the chords inclined on the same angle to the radius or diameter of a circle are equal in length.
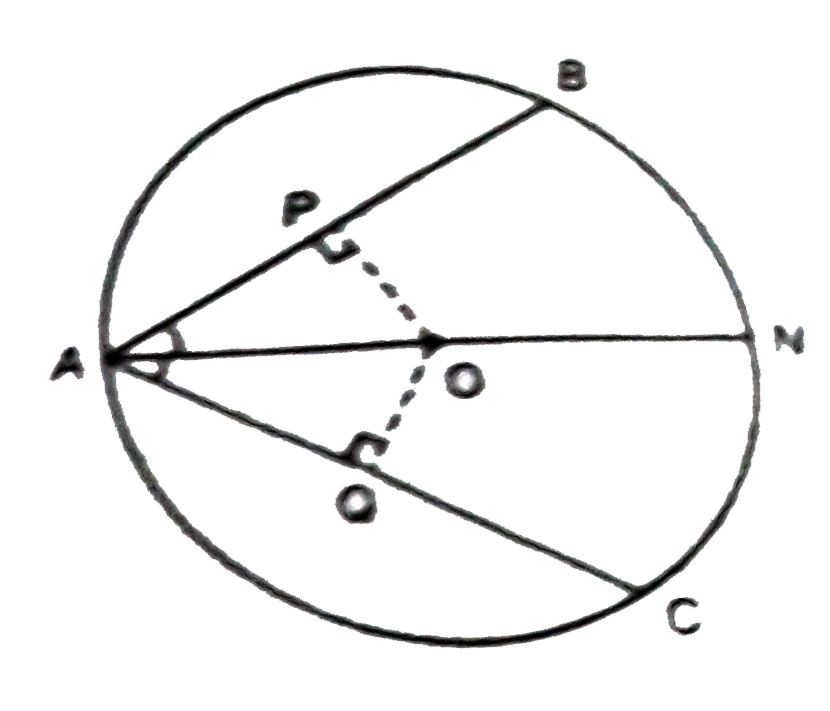
View SolutionIf two equal chords of a circle in intersect within the circle, prove that : the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionIn an isosceles triangle, prove that the angles opposite to equal sides are equal.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionProve that the angle in a segment greater than a semi-circle is less than a right angle.
View SolutionProve that the angle in a segment greater than a semi-circle is less than a right angle.
View Solution
