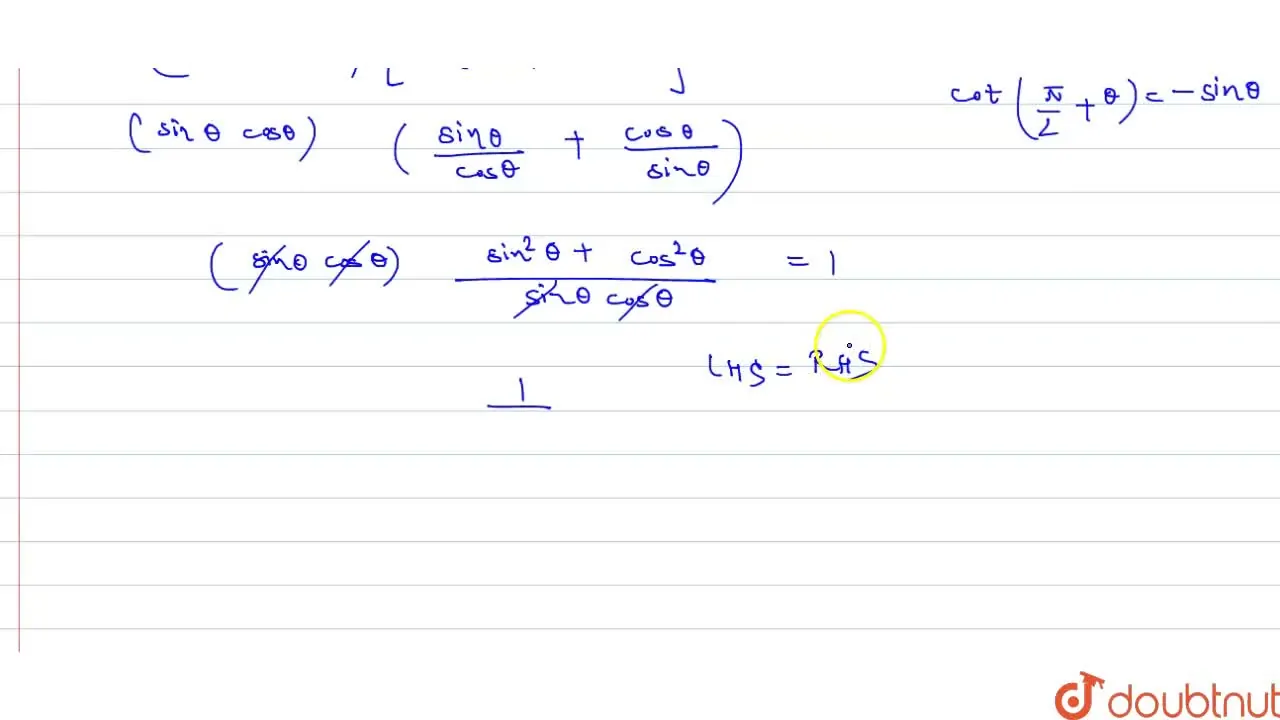cos(3π2+θ)cos(2π+θ)×[cot(3π2−θ)+cot(2π+θ)]=?
A
0
B
1
C
sinθ
D
cosθ
Video Solution
Text Solution
The correct Answer is:B
We have
cos (3π2+θ)cos (2π+θ)[cot (3π2−θ)+ cot (2π+θ)]
= cos (π+(π2+θ)] cos (2π+θ)[ cot {π+(π2−θ)} cot (2π+θ)]
=− cos (2π2 cos θ)[ cot (π2=θ)+ cot θ]
[∵ cos (π+x)= cos x , cot (π+x)= cot x and cot (2π+x) cot x ]
= sin θ cos θ[ tan θ+ cot θ][∵ cos (π2+θ)=− sin θ]
=( sin θ cot θ)[sin θcos θ+ cos θsin θ]=(sin θ cos θ).(sin2θ cos2θ)(sin θ cos θ)=1
|
Updated on:21/07/2023
Related Playlists
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC , OR CIRCULAR, FUNCTIONSEXERCISE - Exercise (15A)10videos
TRIGONOMETRIC , OR CIRCULAR, FUNCTIONS
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC , OR CIRCULAR, FUNCTIONSEXERCISE - Exercise (15B)20videos
TRIGONOMETRIC , OR CIRCULAR, FUNCTIONS
- BOOK - RS AGGARWALCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - EXERCISE 26 C13videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - EXERCISE21videos
TRIGONOMETRIC EQUATIONS
Similar Questions
cos(3π2+θ)⋅cos(2π+θ)=
View SolutionWhat is the value of cos(3π2+θ)cos(2π+θ)[cot(3π2−θ)+cot(2π÷θ)]?
View Solutioncot(3π2−θ)+cot[2π+θ]=
View Solutiontan(πcosθ)=cot(πsinθ)
View Solutionsin(π2+θ)⋅cos(3π2+θ)⋅tan(5π2+θ)⋅cot(7π2+θ)
View SolutionIf −π2<θ<π2 and θ≠±π4, then the value of cot(π4+θ)cot(π4−θ) is
View SolutionSolve tan(π2cosθ)=cot(π2sinθ)
View Solutionxcot(π2+θ)+tan(π2+θ)sinθ+csc(π2+θ)=0
View SolutionIf :cotθ+cot(π4+θ)=2, then : θ =
View SolutionFind cos(π2+θ)+cos(3π2+θ)+cos(5π2+θ)+cos(7π2+θ)..... upto 2021 terms
View Solution