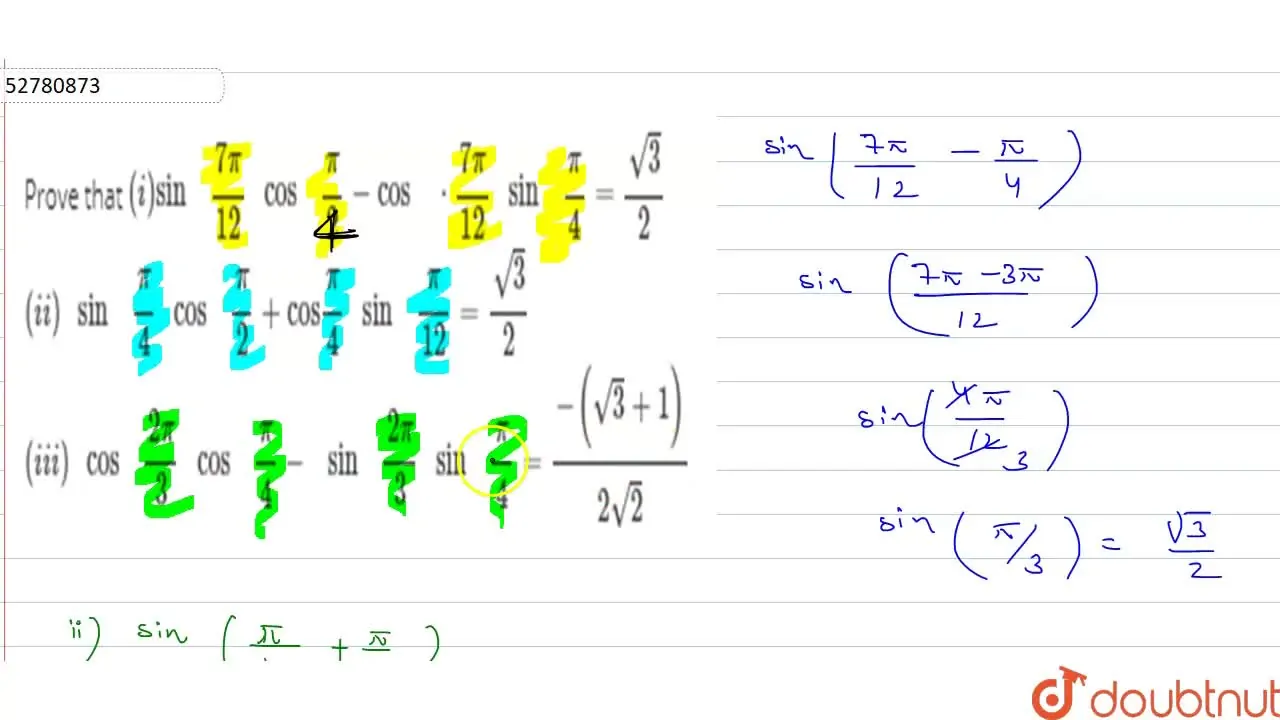
Prove that (i)sin 7π12 cos π2−cos ⋅7π12 sin π4=√32(ii) sin π4 cos π2+cosπ4 sin π12=√32 (iii) cos 2π3 cos π4− sin 2π3 sin π4=−(√3+1)2√2
(i) sin 7π12 cos π2− cos 7π12 sin π4
= sin (7π12−π4) [∵ sin x cos y - cos x sin y = sin ( x-y) ]
= sin π3=√32
(ii)sin π4 cos π12+ cos π2sin π12
= sin (π2+π12) [∵sin x cos y + cos x sin y = sin (x + y)]
= sin π3=√32
(iii) sin 2π3 cos π4−sin 2π3 sin π4
= cos (π−π3) cos π4− sin (π−π3) sin π4
=− cos π3 cos π4− sin π3 cos π4
[∵ sin (π−x) = sin x , cos (π−x)=− cos x]
=(−12×1√2)−(√32×1√2)=−⎧⎪
⎪⎨⎪
⎪⎩(√3+1)2√2⎫⎪
⎪⎬⎪
⎪⎭.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC , OR CIRCULAR, FUNCTIONSEXERCISE - Exercise (15A)10videos
TRIGONOMETRIC , OR CIRCULAR, FUNCTIONS
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC , OR CIRCULAR, FUNCTIONSEXERCISE - Exercise (15B)20videos
TRIGONOMETRIC , OR CIRCULAR, FUNCTIONS
- BOOK - RS AGGARWALCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - EXERCISE 26 C13videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - EXERCISE21videos
TRIGONOMETRIC EQUATIONS
Similar Questions
sinπ4cosπ12−cosπ4sinπ12 is equal to
View Solutionsinπ4cosπ12−cosπ4sinπ12 is equal to
View SolutionProve that
(i) 2sin 5π12 sin π12=12
(ii) 2 cos 5π12 cos .π12=12
(iii) 2 sin .5π12 cos π2=(2+√32)View SolutionProve that (i) sin .π6. cos .π6=√34 (iii)cos2.π2−sin2.π2=√32
View Solutionsinπ4cosπ12−cosπ4sinπ12 is equal to
View SolutionProve that
(i) cos (π4+x)+ cos (π4−x)=√2 cos x
(ii) cos (3π4+x)−cos (3π4−x)=−√2 sin xView SolutionProve that
(i) tan2.π3+2cos2.π4+3sec2.π6+4cos2.π2=8
(ii) sin .π6 cos 0 + sin .π4 cos .(π)(4)+ sin .π3cos .π6=74
(iii) 4sin π6 sin2π3+3 cos .π3 tan .π4= cosec2.π2=4View Solutioncosπ12−sinπ12=1√2
View SolutionProve that
(i)cos (π3+x)=12( cos x−√3sinx)
(ii) sin (π4+x)+ sin (π4−x)=√2 cos x
(iii)1√2 cos ((pi)/(4) + x) = (1)/(2) (cosx−sinx)
(iv) cos x + cos (2π3+x)+ cos (2π3−x)=0View Solutionsin(π2)=2sin(π4)cos(π4)
View Solution