Prove that √sec2θ+cosec2θ=tanθ+cotθ.
Video Solution
Text Solution
LSH =√sec2θ+cosec2θ
=√1cos2θ+1sin2θ [∴secθ=1cosθ and cosecθ=1sinθ]
=√sin2θ+cos2θsin2θ.cos2θ=√1sin2θ.cos2θ [∴sin2θ+cos2θ=1]
=1sinθ.cosθ=sin2θ+cos2θsinθ.cosθ [∴1=sin2θ+cos2θ]
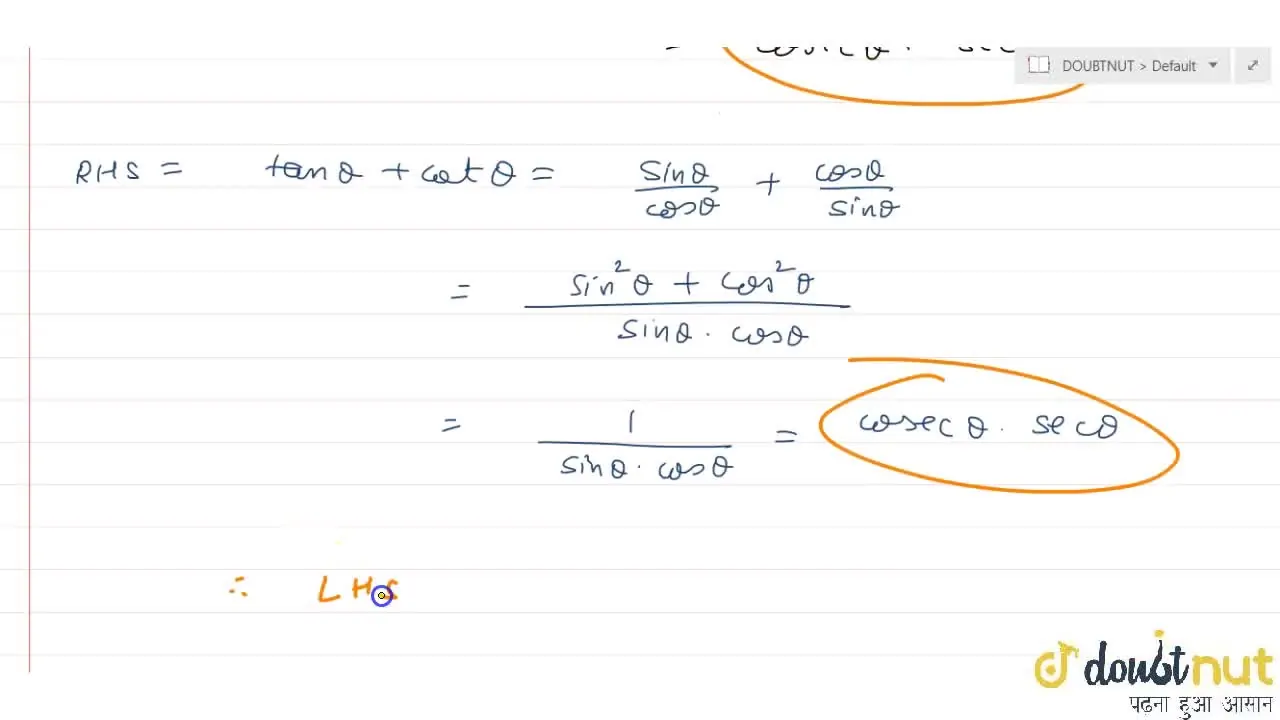
=sin2θsinθ.cosθ+cos2θsinθ.cosθ
=sinθcosθ+cosθsinθ [∴tanθ=sinθcosθ and cotθ=cosθsinθ]
=tanθ+cotθ=RHS
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Prove that
√sec2θ+cosec2θ=tanθ+cotθ.View SolutionProve: √sec2θ+cosec2θ=tanθ+cotθ.
View SolutionProve that : √(1−cos2θ)sec2θ=tanθ
View SolutionProve that sec2θ+cosec2θ=sec2θ⋅cosec2θ
View SolutionProve that sec2θ+cosec2θ=sec2θcosec2θ
View SolutionProve that: sec2θ+cosec2θ=cosec2θ.sec2θ .
View SolutionProve that: sec2θ+cosec2θ=sec2θ×cosec2θ.
View SolutionProve that: (1+cotθ−cosecθ)(1+tanθ+secθ)=2
View SolutionProve that : sec2θ+cosec2θ=sec2θ⋅cosec2θ
View SolutionProve that cosec2θ+sec2θcosec2θ−sec2θ=1+tan2θ1−tan2θ
View Solution