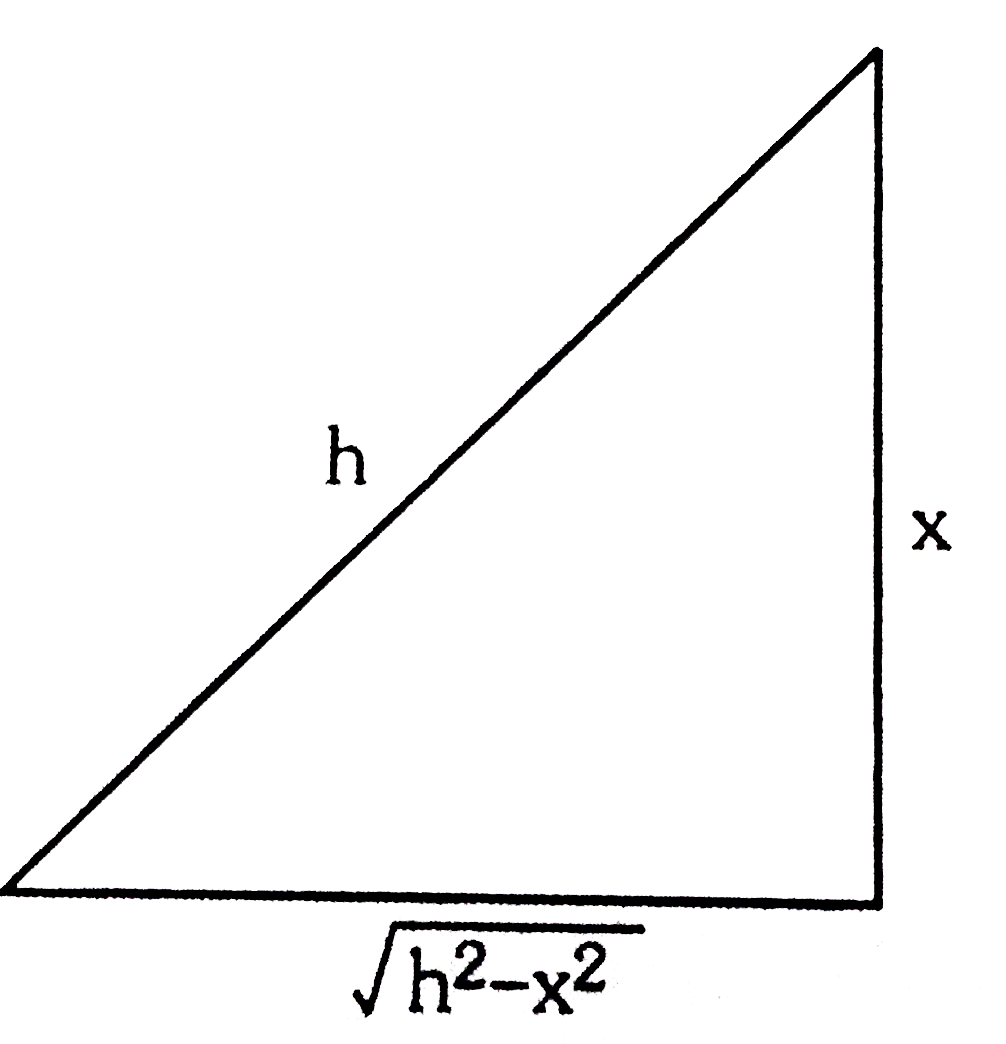
सिद्ध कीजिए कि दिये गये समकोण त्रिभुज का क्षेत्रफल अधिकतम है यदि त्रिभुज समद्विबाहु है ।
यदि A त्रिभुज का क्षेत्रफल है , तब
A=12x√h2−x2
यहाँ h त्रिभुज का कर्ण है तथा x शीर्ष लम्ब है ।
अब dAdx=12{x.12(h2−x2)−1/2(−2x)+√h2−x2}
=12(h2−2x2√h2−x2)
व d2Adx2
=(√h2−x2)(−4x)−(h2−2x2)⋅12(h2−x2)−12(−2x)2(h2−x2)
=(2x3−3xh2)2(h2−x2)3/2
अब , माना dAdx=0, तब
12(h2−2x2)√h2−x2=0⇒h2−2x2=0
⇒x=h√2
अब , [d2ydx2]x=h√2पर =2[(h√2)3−3h3√2]2(h2−h22)3/2=−2<0
अतः x=h√2 उच्चिष्ठ बिंदु है ।
त्रिभुज का आधार =√h2−x2
=√h2−h22=h√2=x ( लम्ब )
अतः त्रिभुज समद्विबाहु है ।
Related Playlists
- BOOK - BALAJI PUBLICATIONCHAPTER - उच्चिष्ठ एवं निम्निष्ठEXERCISE - अभ्यास प्रश्न 11.118videos
उच्चिष्ठ एवं निम्निष्ठ
- BOOK - BALAJI PUBLICATIONCHAPTER - उच्चिष्ठ एवं निम्निष्ठEXERCISE - अभ्यास प्रश्न 11.214videos
उच्चिष्ठ एवं निम्निष्ठ
- BOOK - BALAJI PUBLICATIONCHAPTER - उच्चिष्ठ एवं निम्निष्ठEXERCISE - स्वमूल्यांकन परीक्षण19videos
उच्चिष्ठ एवं निम्निष्ठ
- BOOK - BALAJI PUBLICATIONCHAPTER - आव्यूह EXERCISE - स्वमूल्यांकन परिक्षण17videos
आव्यूह
- BOOK - BALAJI PUBLICATIONCHAPTER - खण्डश: समाकलन EXERCISE - स्वमूल्यांकन परीक्षण28videos
खण्डश: समाकलन
Similar Questions
x के किन मानों के लिये फलन उच्चिष्ठ अथवा निम्निष्ठ है ?
x3−3x2−9x04:55View Solution80 को ऐसे दो भागों में विभाजित कीजिये कि के भाग के घन तथा दूसरे भाग की पाँचवीं घात का गुणनफल महत्तम हो ।
04:48View Solution[0,2π]पर x+sin2x का उच्चतम और निम्नतम मान ज्ञात कीजिए।
05:40View Solutionप्रारंभिक स्तम्भ रूपांतरणों के प्रयोग द्वारा आव्यूह A=⎡⎢⎣012123311⎤⎥⎦ का व्युत्क्रम ज्ञात कीजिए।
03:54View Solutionx sin x का समाकलन कीजिए-
04:17View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है । यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2)है , तो त्रिभुज की शेष दो भुजाओ के समीकरण ज्ञात कीजिए ।
05:20View Solutionएक सरल रेखा , अक्षो के साथ ऐसा समकोण त्रिभुज बनातीं है कि जिसके कर्ण कि लम्बाई √53 तथा क्षेत्रफल 7 वर्ग इकाई है । रेखा का समीकरण ज्ञात कीजिए
06:21View Solutionसिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है यदि
∣∣ ∣ ∣∣1111+cosA1+cosB1+cosCcos2A+cosAcos2B+cosBcos2C+cosC∣∣ ∣ ∣∣=001:04:04View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
01:46:57View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
08:24View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है। यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2) हो तो त्रिभुज की शेष दो भुजाओं के समीकरण ज्ञात कीजिए।
02:48View Solutionयदि A, B, C, D समष्टि (space) में चार बिन्दु हैं, तो सिद्ध कीजिए कि |AB×CD+BC×AD+CA×BD|=4 ( त्रिभुज ABC का क्षेत्रफल )
04:24View Solutionत्रिभुज का क्षेत्रफल | उदाहरण
02:37View SolutionRevision|त्रिभुज का क्षेत्रफल
02:50View Solutionकिसी समद्विबाहु समकोण त्रिभुज का परिमाप 2012 है तब इसका क्षेत्रफल होगा -
01:15View SolutionThe hypotenuse of a right-angled triangle is 39 cm and the difference between the other two sides is 21 cm. The area of this triangle is :
किसी समकोण त्रिभुज का कर्ण 39 cm है और अन्य दो भुजाओं का अंतर 21 cm है, तो त्रिभुज का क्षेत्रफल है?43:44View Solution


