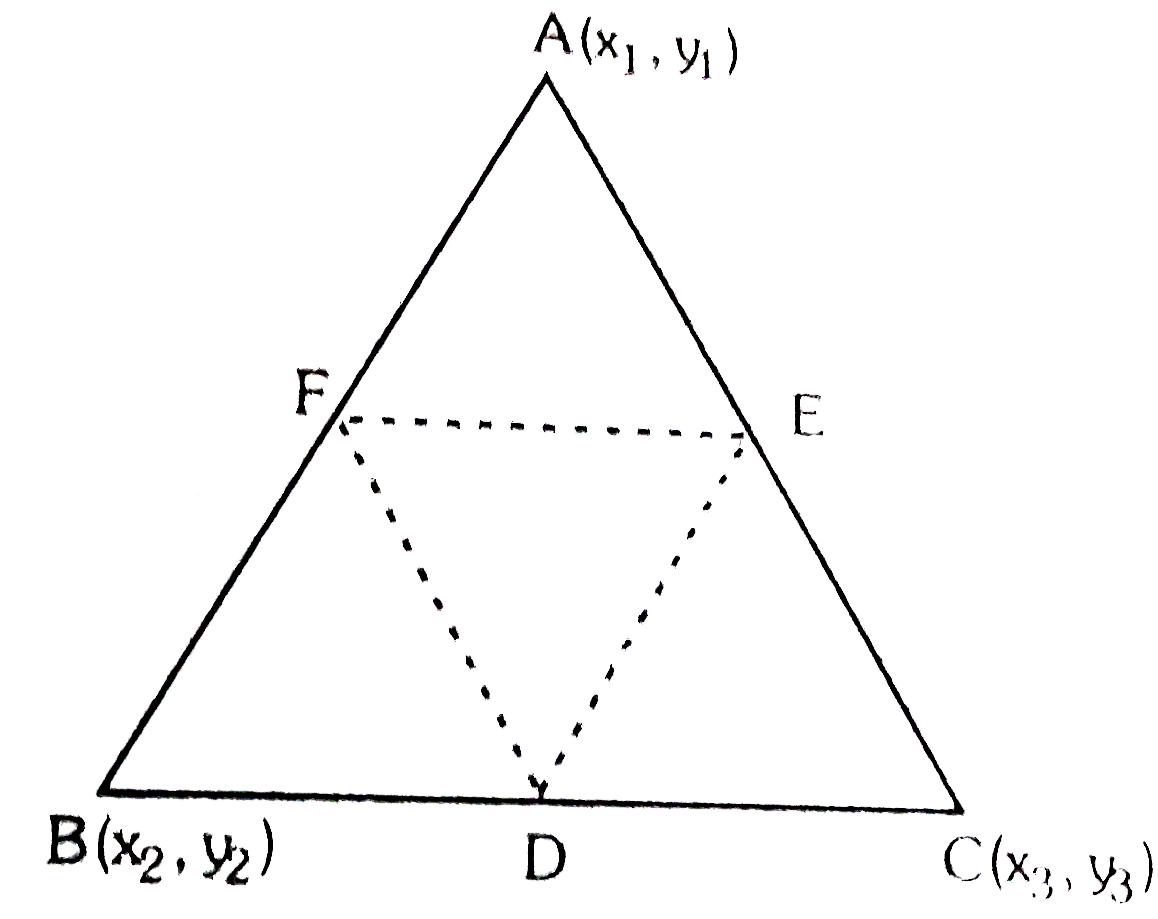
सिद्ध कीजिए कि किसी त्रिभुज का केन्द्रक वही है जो उसकी भुजाओं के मध्य बिंदुओं को मिलाने से बने त्रिभुज का होता है |
माना के शीर्ष तथा है | इसके केन्द्रक के निर्देशांक
प्रश्नानुसार, माना D,E,F क्रमशः भुजाओं BC,CA तथा AB के मध्य बिन्दु है |
तब,
अब का केन्द्रक
स्पष्टतः व एक ही बिन्दु को व्यक्त करते है |
Related Playlists
- BOOK - BALAJI PUBLICATIONCHAPTER - समकोणीय कार्तीय निर्देशांक निकाय EXERCISE - अभ्यास प्रश्न 13.122videos
समकोणीय कार्तीय निर्देशांक निकाय
- BOOK - BALAJI PUBLICATIONCHAPTER - समकोणीय कार्तीय निर्देशांक निकाय EXERCISE - NCERT प्रारूप प्रश्न4videos
समकोणीय कार्तीय निर्देशांक निकाय
- BOOK - BALAJI PUBLICATIONCHAPTER - शंकु परिच्छेदः वृतEXERCISE - स्वमूल्यांकन परीक्षण ((B) विवेचनात्मक सोच वाले प्रश्न )3videos
शंकु परिच्छेदः वृत
- BOOK - BALAJI PUBLICATIONCHAPTER - समुच्चय EXERCISE - विवेचनात्मक सोच वाले प्रश्न5videos
समुच्चय
Similar Questions
एक आयत के तीन शीर्ष (0,0)(2,0) तथा (0,3) है | सिद्ध कीजिए चौथे शीर्ष के निर्देशांक (2,3) होंगे |
07:05View Solutionकार्तीय तल में एक चतुर्भुज जिसके शीर्ष (−4,5),(0,7),(5,−5) और (−4,−2) है | इसका क्षेत्रफल भी ज्ञात कीजिए |
03:53View Solutionसिद्ध कीजिए की तीन वृतों x2+y2−4x−6y−12=0, x2+y2+2x+4y−10=0 तथा x2+y2−10x−16y−1=0 के केंद्र संरेखाय हैं।
06:09View Solutionदो परिमित समुच्चों m में n है, प्रथम समुच्चय के उपसमुच्चायों की कुल संख्या, द्वितीय समुच्चय के उपसमुच्चयों से 56 अधिक है, m व n के मान ज्ञात कीजिए।
07:31View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
01:21View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिंदु(1,2) से होकर जाती है जिसके द्वारा अक्षो से बने त्रिभुज का क्षेत्रफल 92 वर्ग इकाई है
02:54View Solutionकिसी त्रिभुज के शीर्षो के निर्देशांक (2,5),(6−2) तथा (−3,−4) है , तो उसकी मध्यिकाओ के समीकरण ज्ञात कीजिए
04:17View Solutionकिसी त्रिभुज कि भुजाओ के मध्य बिन्दुओ के निर्देशांक क्रमशः (2,1),(−5,7) तथा (−5,5) है त्रिभुज कि भुजाओ के समीकरण ज्ञात कीजिए ।
03:51View Solutionत्रिभुज का गुरुत्व केंद्र होता है।
06:19View Solutionवह त्रिभुज जिसका लांबकेंद्र त्रिभुज का शीर्ष बिंदु होता है ,कहलाता है -
05:13View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
06:38View Solutionसिद्ध कीजिए कि किसी गुणोत्तर श्रेढ़ी के आरम्भ और अंत से संदुररस्थ पदों का गुणनफलन सदैव अचर रहता है ।
03:17View Solutionयदि किसी त्रिभुज की भुजाओं के मध्य - बिंदुओं के निर्देशांक (2,1),(−1,−3) और (4,5) हों , तो उसके शीर्षों के निर्देशांक ज्ञात कीजिए ।
04:56View Solutionबिंदुओं (0,0),(0,8) और (4,6) से बने त्रिभुज का केन्द्रक और परिकेन्द्र ज्ञात कीजिए ।
01:40View Solutionबिंदुओं (−3,−1),(−1,3) और (6,2) से बने त्रिभुज के परिकेन्द्र के निर्देशांक ज्ञात कीजिए ।
04:32View Solutionकिसी त्रिभुज के शीर्ष बिन्दुओं के निर्देशांक (0,1),(2,0) और (-1,-2) है। उसकी भुजाओं के समीकरण ज्ञात कीजिए।
06:40View Solution


