Question

Prove that the least positive value of $x,$
satisfying $\tan x=x+1,lie\sin the\in terval(\frac{\pi }{4},\frac{\pi }{2})\stackrel{.}{}$

Explanation

Let `f(x)=tan x " and " g(x)=x+1,` which can be shown as follows.

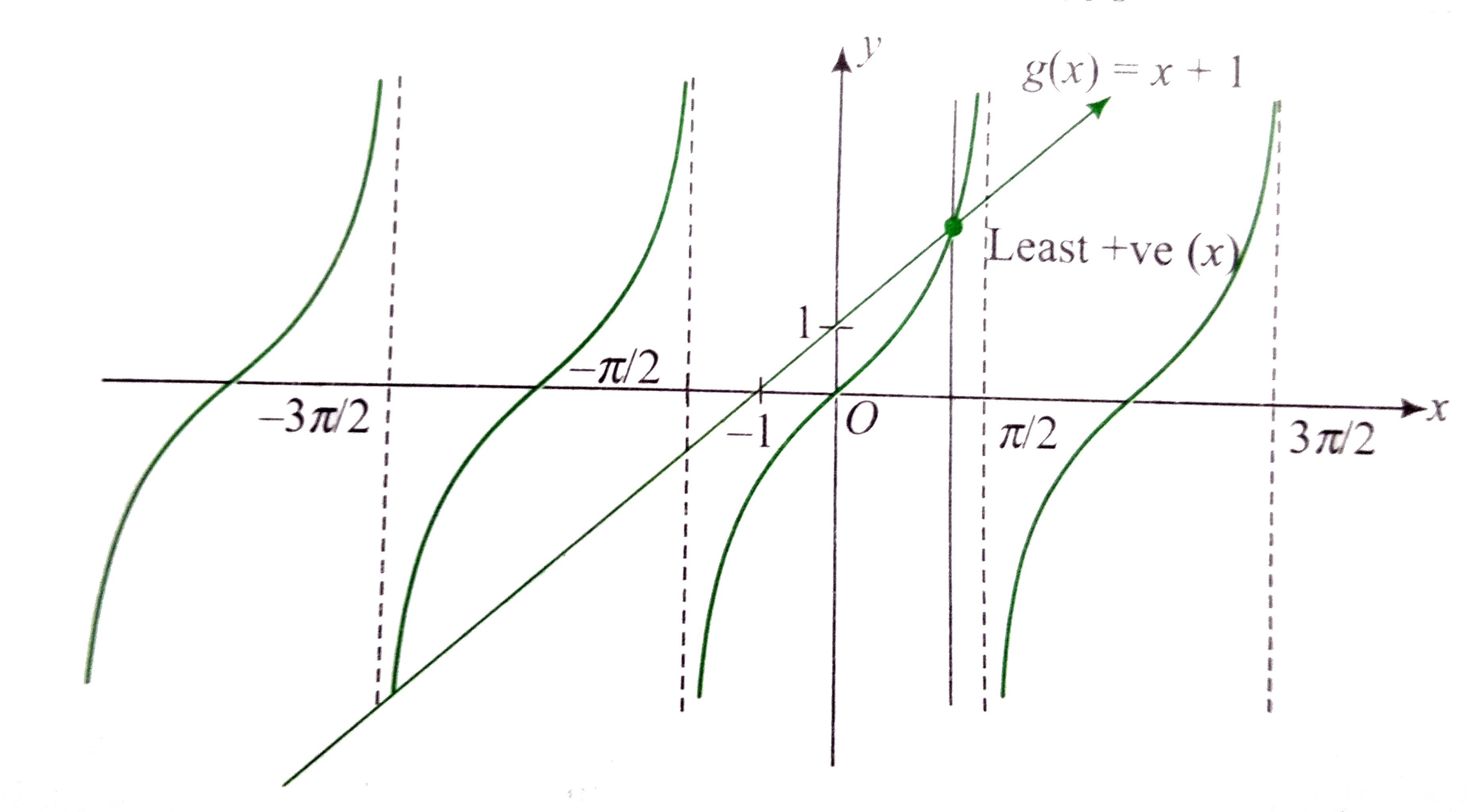
From the figure, `tanx =x+1` has infinitely many solutions but the least positive value of x lies in `((pi)/(4),(pi)/(2)).`