Prove that the line segments joints joining the mid-points of the adjacent sides of a quadrilateral from a parallelogram.
Step by step video & image solution for Prove that the line segments joints joining the mid-points of the adjacent sides of a quadrilateral from a parallelogram. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Using vector method, prove that the line segments joining the mid-points of the adjacent sides of a quadrilateral taken in order form a parallelogram.
View SolutionProve that the figure formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
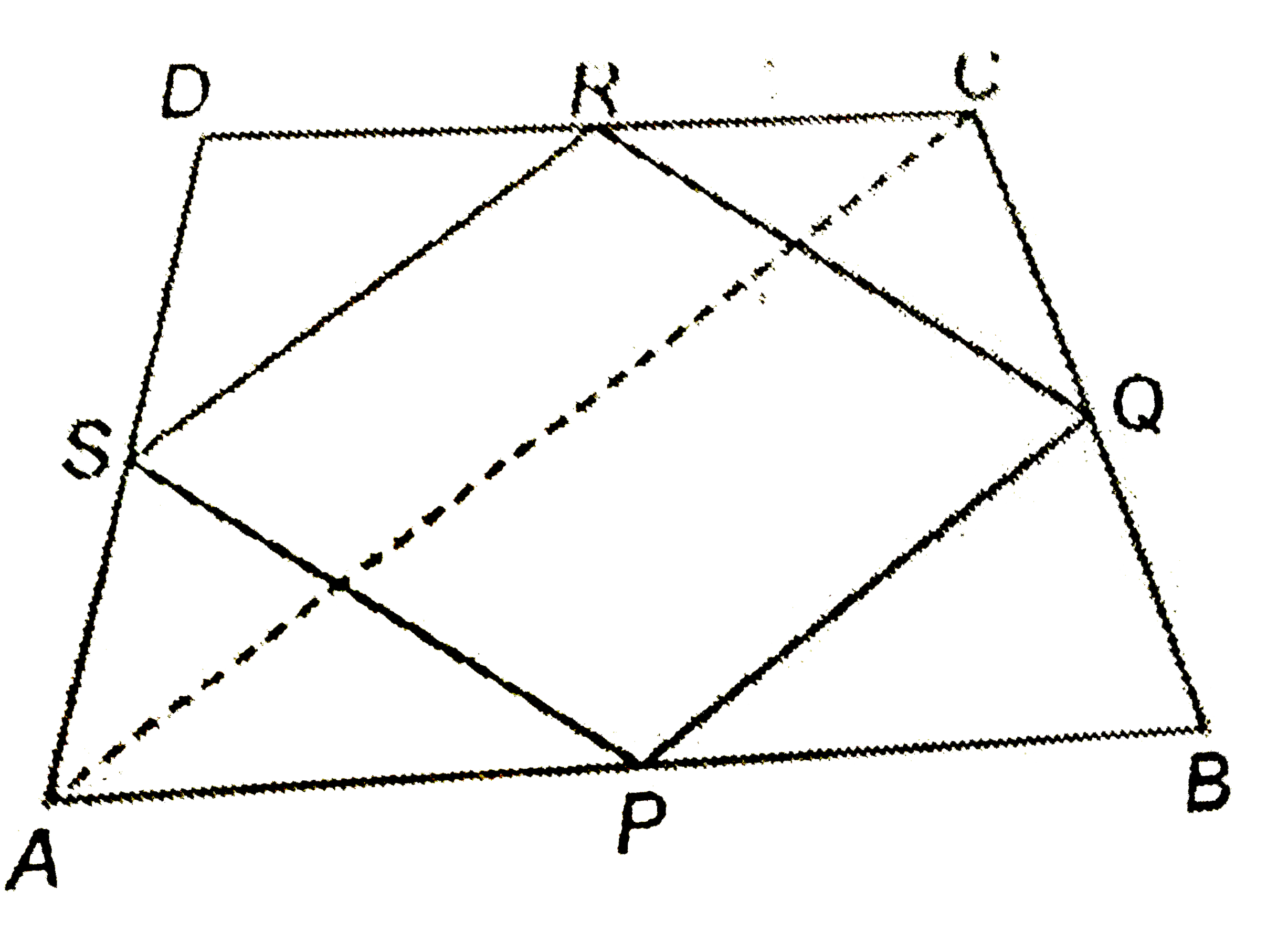 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The line segments joining the midpoints of the adjacent sides of a quadrilateral form
Aa parallelogramBa rectangleCa squareDa rhombus - Question 2 - Select One
The meeting point of adjacent sides of a quadrilateral is called a___
AVertexBSideCcornerDSegment
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
View SolutionShow that the line segments joining the mid-points of opposite sides of a quadrilateral bisects each other.
View SolutionThe figure formed by joining the mid-points of the adjacent sides of a quadrilateral is a parallelogram (b) rectangle square (d) rhombus
View SolutionThe figure formed by joining the mid-points of the adjacent sides of a quadrilateral is a parallelogram (b) rectangle (c) square (d) rhombus
View SolutionProve that the quadrilateral formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
View Solution

