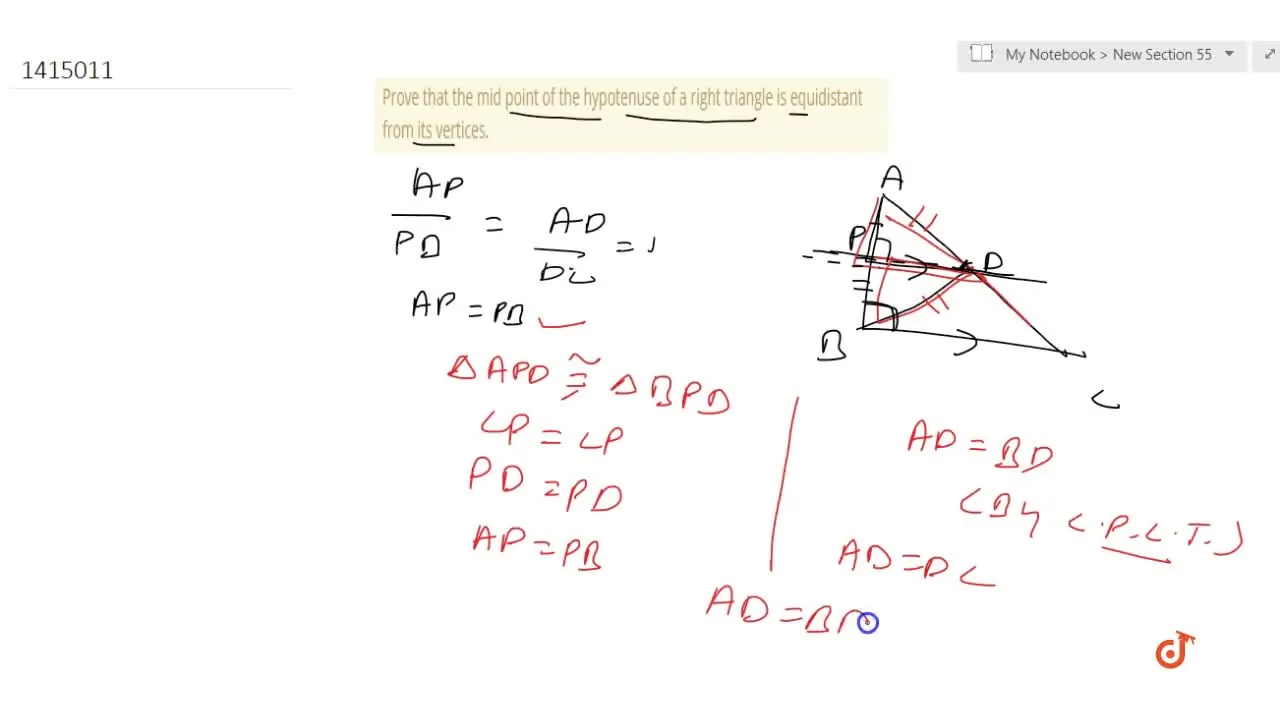
Prove that the mid point of the hypotenuse of a right triangle is equidistant from it vertices.
Given : A Δ ABC in wchih ∠BAC=90∘ and O is the midpoint of BC
To Prove : OA = OB = OC
Construction : Draw a circle with O as centre and OB as radius.
Proof : Clearly, this circle with O as centre and OB as radius and this circle will pass through B as well as C.
If possible, suppose this circle does not through A. Let it meet BA or BA produced at A'.
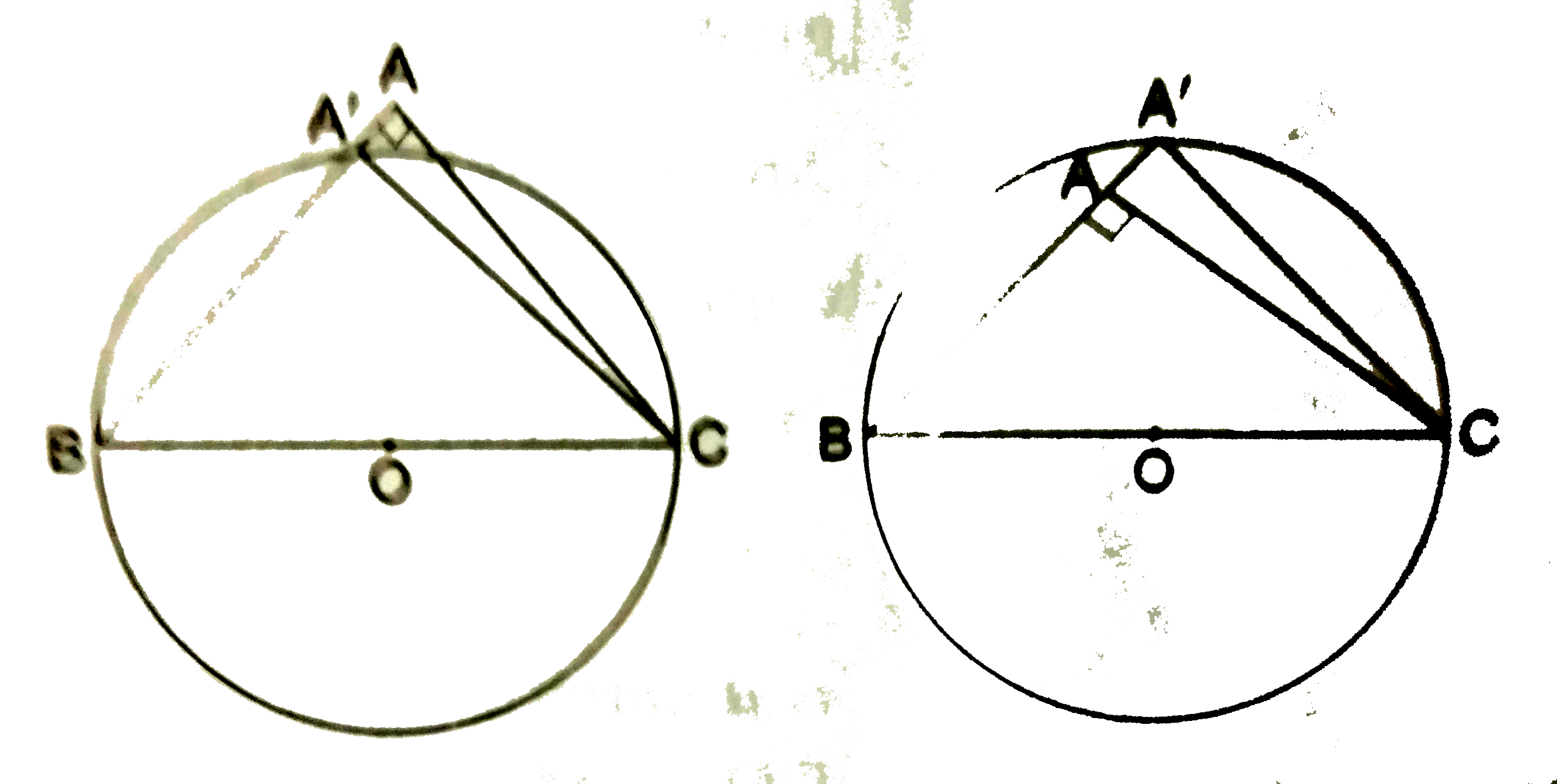
The, ∠BA'C=90∘ [ angle in a semicircle ] .
But, ∠BAC=90∘ [given]
∴∠BA'C=∠BAC. .....(i )
But, this is wrong since an exterior angle of a triangle cannot be equal to its interior opposite angle.
This can be true only when A'coincides with A.
Thus, the above circle which passes through B and C must also pass through A.
∴OA=OB=OC.
Similar Questions
Prove that the mid-point of the hypotenuse of a right triangle is equidistant from its vertices
View SolutionProve that the mid-point of the hypotenuse of right angled triangle is equidistant from its vertices.
View SolutionProve by the vector method that the mid-point of the hypotenuse of a right angled triangleis equidistant from the vertices of the triangle.OR
View SolutionIn Fig. 14.40, a right triangle BOA is given. C is the mid-point of the hypotenuse AB . Show that it is equidistant from the vertices O, A and B . (FIGURE)
View SolutionWhat is the measure of the hypotenuse of a right triangle, when its medians, drawn from the vertices of the acute angles, are 5 cm and 2√10 cm long ?
View SolutionWhat is the measure of the hypotenuse of a right triangle, when its medians, drawn from the vertices of the acute angles, are 5 cm and 2√10cm
View SolutionProve that the line segment joining the mid-point of the hypotenuse of a right triangle to its opposite vertex is half of the hypotenuse.
View SolutionProve by vector method, that in a right-angled triangle ABC, AB2+AC2=BC2, the angle A being right angled. Also prove that mid-point of the hypotenuse is equidistant from vertex.
View SolutionWhat is the number of points in the plane of a triangle ABC which are at equal distance from the vertices of the triangle ?
View SolutionA point on the hypotenuse of a right triangle is at distances a and b from the sides of the triangle. Show that the minimum length of the hypotenuse is (a23+b23)32
View Solution