Question

Prove using similar triangles, that a line drawn through the mid-point of one side of a triangle parallel to another side, bisects the third side.

Explanation

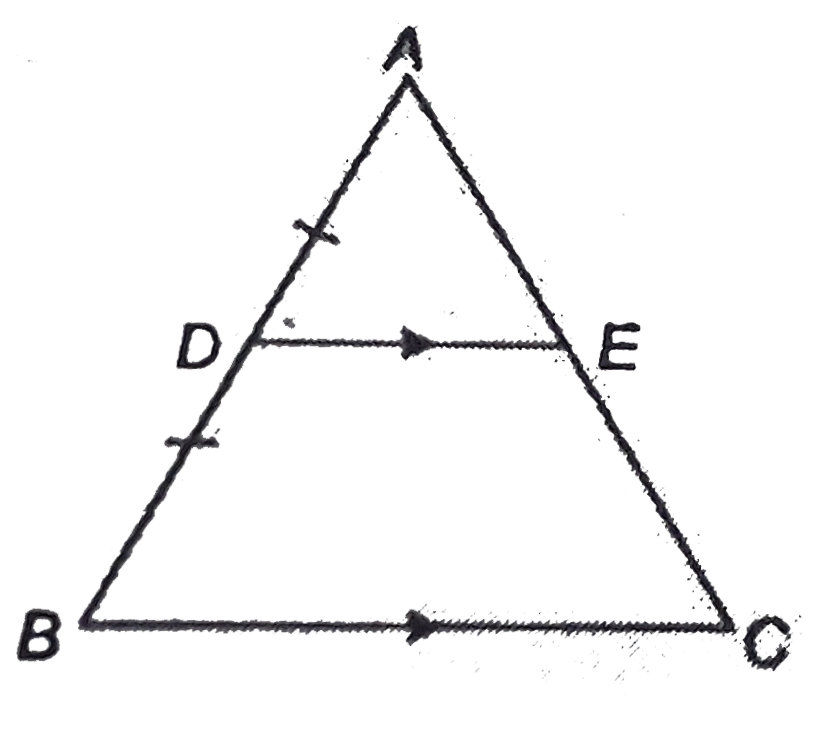
Given : ` DeltaABC` in which D is the mid-point of AB and DE is drawn parallel to BC, meeting AC in E.
To prove : AE= EC
proof: Since DE||BC
By basic proportionality theorem, we have
` (AD)/(DB) = (AE)/(EC) ….. (1)`
but AD=DB (D is the mid - point )
` (AD)/(DB)= (AD)/(AD)=1`
from (1) and (2),we have
`(AE)/(EC) = 1 `
` Rightarrow AE= EC`