Representation of sets
What is Representation of sets?
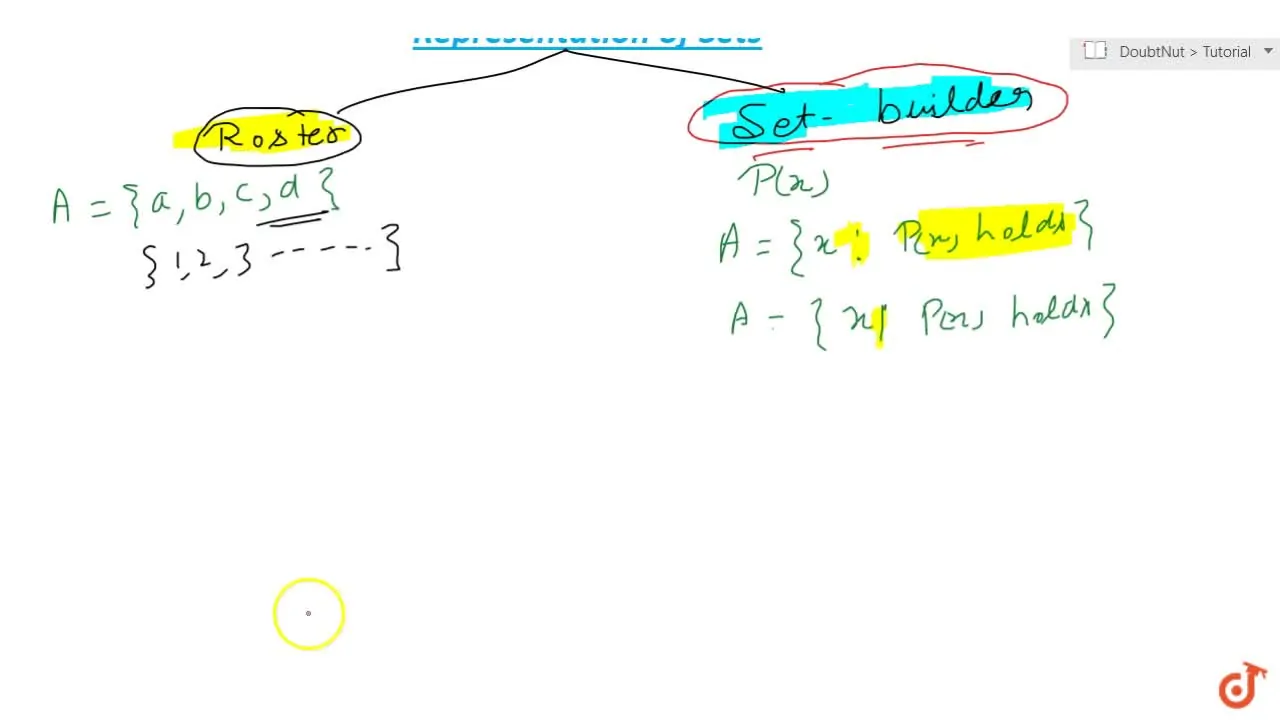
When it comes to the representation of a set, the following three methods are commonly used:
(i) Statement form method
(ii) Roster or tabular form method
(iii) Rule or set builder form method
Now let us have a deep look at the different methods:
Statement form
In this, the description of the elements is well-defined where the set is given and the same are enclosed in the form of curly brackets.
For example:
(i) The set of even numbers less than 8 is written as: {even numbers less than 7}.
(ii) A set of volleyball players with ages between 20 years to 30 years.
(iii) A set of students in class IX whose weights are more than your weight
(iv) A set of numbers greater than 30 and smaller than 55.
Roster form or tabular form
In this form, the listing of the elements of the set are done within the pair of brackets { } which are separated by commas.
For example:
(i) Let N indicate the set of first five natural numbers.
Therefore, N = {5, 6, 7, 8, 9} → Roster Form
(ii) The set of all vowels of the English alphabet.
Therefore, X = {a, e, i, o, u} → Roster Form
(iii) W is the set of first four months of the year.
Therefore, W = {January, February, March, April} → Roster Form
(iv) The set of all even numbers less than 9.
Therefore, X = {2, 4, 6, 8} → Roster Form
Set builder form
Here, in order to make the set well defined, a rule is written by making use of the pair of brackets within it. In this case, for becoming the member of that set, a single property must be possessed by all the elements of the set.
Here, the symbol “x” or any other variable are used in order to describe the element of the set. The symbol, “:” is used in order to denote, “such that.” Braces are used to enclose the whole description which defines, “set of all.”
For example:
(i) Let Q is a set of counting numbers greater than 14;
the set Q in set-builder form is written as :
Q= {x : x is a counting number and greater than 14}
or
Q = {x | x is a counting number and greater than 14}
It can be read as, “Q is the set of elements x such that x happens to be a counting number which is greater than 14'.
(ii) Let A denote the set of odd numbers between 5 and 13. We will write it as:
A = {x|x is a odd number, 5 < x < 13}
or A = {x : x ∈ Q, 5 < x < 134 and Q is an even number}
(iii) If X = {3, 4, 5, 6} . This is expressed in roster form.
Now, we will express in set builder form.
X = {x : x is a natural number and 2 < x < 7}
What is the cardinal number of a set?
Cardinal number happens to be the number of distinct elements in a finite set. The expression n(A) is denoted and read as ‘the number of elements of the set’.
For example:
(i) Set A = {1, 4, 7, 9, 12} has 5 elements.
Here, the cardinal number of set A = 5. Thus, it is denoted as n(A) = 5.
(ii) Set B = {a, b, c, d, e ,f} has 6 elements.
In this case, the cardinal number of set B = 6. Here, it is denoted as n(B) = 6.
(iii) Set C = {Australia, New Jersey, California, Switzerland} has 4 elements.
Here, the cardinal number of set C = 4. So, it is denoted as n(C) = 4.
(iv) Set D = {4, 4, 6, 6, 8, 9, 10} has 5 element.
In this case, the cardinal number of set D = 5. So, it is denoted as n(D) = 5.
(v) Set E = { } has got no element.
So, in this case, the cardinal number of set D = 0. Therefore, it is denoted as n(D) = 0.
Solved examples:
1. Find out the cardinal number of each of the following sets:
(i) X = {letters in the word KERALA}
(ii) Y = {4, 6, 7, 7, 8, 9, 9, 10}
Solution:
(i) Given, X = {letters in the word MUMBAI}
Then, X = {M, U, B, A, I}
So, in this case, the cardinal number of set X = 4, i.e., n(X) = 4
(ii) Given, Y = {4, 6, 7, 7, 8, 9, 9, 10}
Then, Y = {4, 6, 7, 8, 9}
Here the cardinal number of set Y = 5, i.e., n(Y) = 5
2. Can you find out the cardinal number of a set from each of the following?
(i) P = {x | x ∈ N and x22 < 30}
(ii) Q = {x | x is a factor of 20}
Solution:
(i) Given, P = {x | x ∈ N and x22 < 30}
Then, P = {1, 2, 3, 4, 5}
In this case, cardinal number of set P = 5, i.e., n(P) = 5
(ii) Given, Q = {x | x is a factor of 20}
Then, Q = {1, 2, 4, 5, 10, 20}
So, here the cardinal number of set Q = 6, i.e., n(Q) = 6.
(i) Statement form method
(ii) Roster or tabular form method
(iii) Rule or set builder form method
(i) The set of even numbers less than 8 is written as: {even numbers less than 7}.
(ii) A set of volleyball players with ages between 20 years to 30 years.
(iii) A set of students in class IX whose weights are more than your weight
(iv) A set of numbers greater than 30 and smaller than 55.
(i) Let N indicate the set of first five natural numbers.
Therefore, N = {5, 6, 7, 8, 9} → Roster Form
Therefore, X = {a, e, i, o, u} → Roster Form
Therefore, W = {January, February, March, April} → Roster Form
Therefore, X = {2, 4, 6, 8} → Roster Form
Here, the symbol “x” or any other variable are used in order to describe the element of the set. The symbol, “:” is used in order to denote, “such that.” Braces are used to enclose the whole description which defines, “set of all.”
the set Q in set-builder form is written as :
Q= {x : x is a counting number and greater than 14}
or
Q = {x | x is a counting number and greater than 14}
It can be read as, “Q is the set of elements x such that x happens to be a counting number which is greater than 14'.
A = {x|x is a odd number, 5 < x < 13}
or A = {x : x ∈ Q, 5 < x < 134 and Q is an even number}
Now, we will express in set builder form.
X = {x : x is a natural number and 2 < x < 7}
Here, the cardinal number of set A = 5. Thus, it is denoted as n(A) = 5.
In this case, the cardinal number of set B = 6. Here, it is denoted as n(B) = 6.
Here, the cardinal number of set C = 4. So, it is denoted as n(C) = 4.
In this case, the cardinal number of set D = 5. So, it is denoted as n(D) = 5.
So, in this case, the cardinal number of set D = 0. Therefore, it is denoted as n(D) = 0.
Solved examples:
(i) X = {letters in the word KERALA}
(ii) Y = {4, 6, 7, 7, 8, 9, 9, 10}
(i) Given, X = {letters in the word MUMBAI}
Then, X = {M, U, B, A, I}
So, in this case, the cardinal number of set X = 4, i.e., n(X) = 4
Then, Y = {4, 6, 7, 8, 9}
Here the cardinal number of set Y = 5, i.e., n(Y) = 5
(ii) Q = {x | x is a factor of 20}
(i) Given, P = {x | x ∈ N and x22 < 30}
Then, P = {1, 2, 3, 4, 5}
In this case, cardinal number of set P = 5, i.e., n(P) = 5
Then, Q = {1, 2, 4, 5, 10, 20}
So, here the cardinal number of set Q = 6, i.e., n(Q) = 6.
Similar Questions
What is Set ?? Representation of set and Different type of sets
View SolutionSets|Well - Defined Collections|Not Well - Defined Collections|Question|Representation Of A Sets|Roster Or Tabular Form|Concepts|Questions|Set Builder Form|Question|Summary
View SolutionRepresentation of a Relation in(a) set builder form
View SolutionMake a graphical r lake a graphical representation of the set of constraints the following LPP Maximize Z=x+y Subject to the constraints 5x+10y≤5,x+y>=1,y≤4,x≥0,y>0. Show that the LPP has unique optimal solution.
View SolutionCartesian Product Of Sets|Exercise Questions|Note|Exercise Questions|Relations|Total Number Of Relations|Exercise Questions|Representation Of Relations|Exercise Questions|OMR
View SolutionCartesian Product Of Two Sets|Exercise Questions|Relation|Exercise Questions|Representation Of Relation|Exercise Questions|Domain And Range Of A Relation|Inverse Relation|OMR
View SolutionRepresentation Of Vectors
View SolutionRepresentation of integers on number line
View SolutionWriting is the … …. representation of speech sounds.
View SolutionWriting is the . . . . . . . . . . .
representation of speech sounds.View Solution