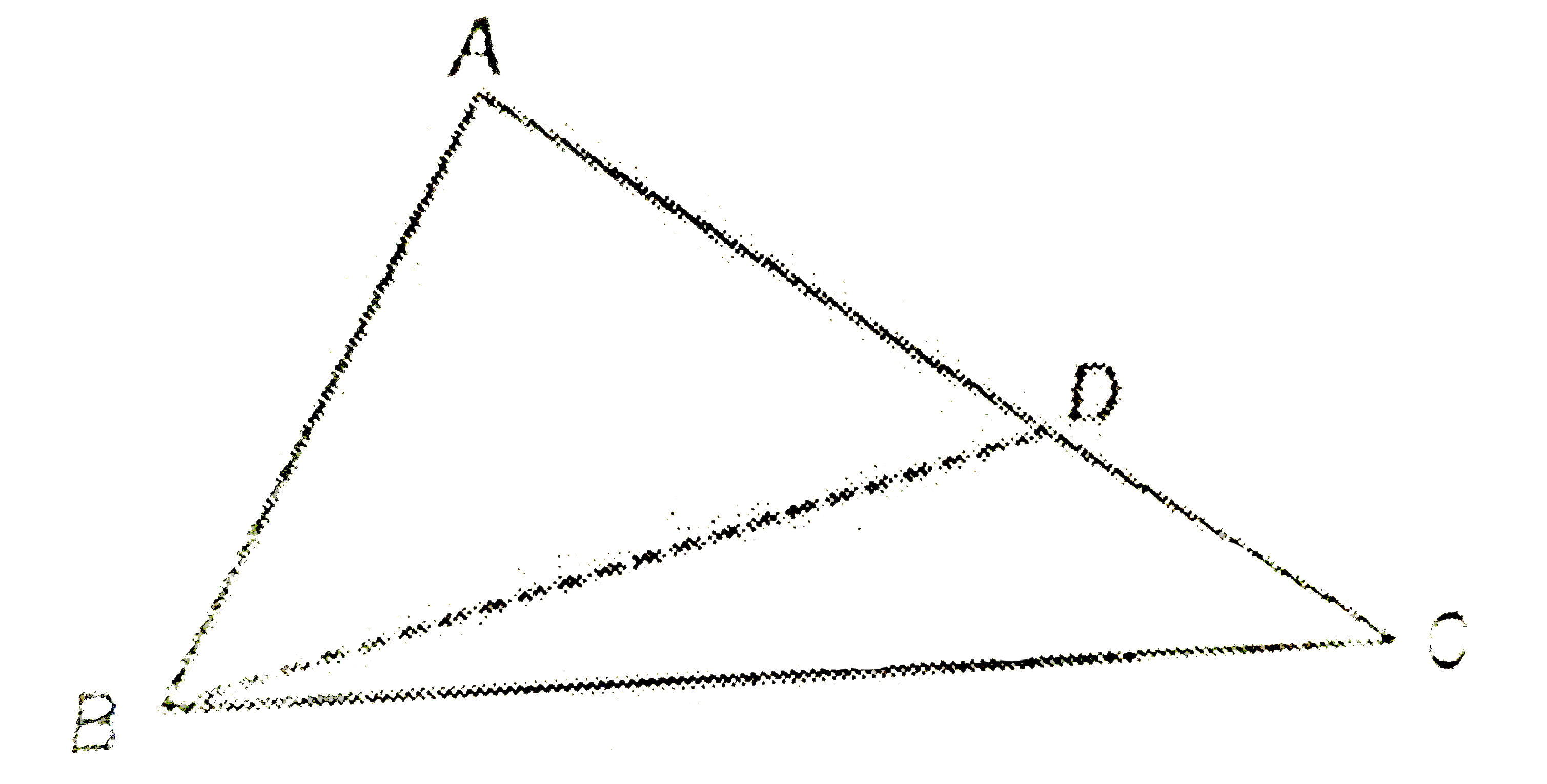
Show that the difference of any two sides of a triangle is less than the third side.
Given : ΔABC in which AC>AB.
To prove : AC−AB<BC
Construction : Cut AB = AD from AC. Join BD. ltbr> Proof : ∠BDC is the exterior angle of ΔABD.
∴∠BDC−∠ABD+∠BAD.
( ∵ the exterior angle is equal t the sum of opposite interior angles of a triangle.)
⇒ ∠BDC>∠ABD ...(1)
Again ∠ADB is the exterior angle of ΔDBC
∴∠ADB=∠DBC+∠BCD
⇒ ∠ADB>∠DBC
but AB=AD
∴∠ABD=∠ADB
Therefore n=∠ABD>∠DBC ...(2)
From (1) and (2), we have
∠BDC<∠DBC
⇒ BC>DC (∵ side opposite to larger angle is larger)
⇒ DC<BC
⇒ AC−AD<BC
⇒ AC−AB<BC (∵AD=AB)
Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 7a
35 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
Fill in the blanks to make the following statements true: In a right triangle the hypotenuse is the ...... side. The sum of three altitudes of a triangle is ......... than its perimeter. The sum of any two sides of a triangle is ......... than the third side. If two angles of a triangle are unequal, then the smaller angle has the ........... side opposite to it. Difference of any two sides of a triangle is ......... than the third side. If two sides of a triangle are unequal, then the larger side has ..... angle opposite to it.
View SolutionWhich of the following statements are true (T) and which are false (F)?
(i) Sum of the three sides of a triangle is less than the sum of its three altitudes.
(ii) Sum of any two sides of a triangle is greater than twice the median drawn to the third side.
(iii) Sum of any two sides of a triangle is greater than the third side.
(iv) Difference of any two sides of a triangle is equal to the third side.
(v) If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it.
(vi) Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.
View SolutionTheorem 7.8 : The sum of any two sides of a triangle is greater than the third side.
View SolutionShow that the sum of the three altitudes of a triangle is less than the sum of three sides of the triangle.
View SolutionShow that the sum of the three altitudes of a triangle is less than the sum of three sides of the triangle.
View SolutionUsing Theorem 6.2, prove that the line joining the mid-point of any two sides of a triangle is parallel to the third side. (Recall that you have done it in class IX).
View SolutionDraw five triangles and measure their sides. Check in each case, if the sum of the lengths of any two sides is always less than the third side.
View SolutionThe line segment joining the mid-points of any two sides of a triangle in parallel to the third side and equal to half of it.
View SolutionProve that the line joining the mid-points of the two sides of a triangle is parallel to the third side.
View SolutionProve analytically that the line segment joining the middle points of two sides of a triangle is equal to half of the third side.
View Solution
