Show that the locus of a point, equidistant from the endpoints of a line segment, is the perpendicular bisector of the segment
Video Solution
Text Solution
The proof will be taken up in two steps.
Step 1 : We initially prove that any point equidistant from the endpoints of a line segment lies on the perpendicular bisector of the line segment.
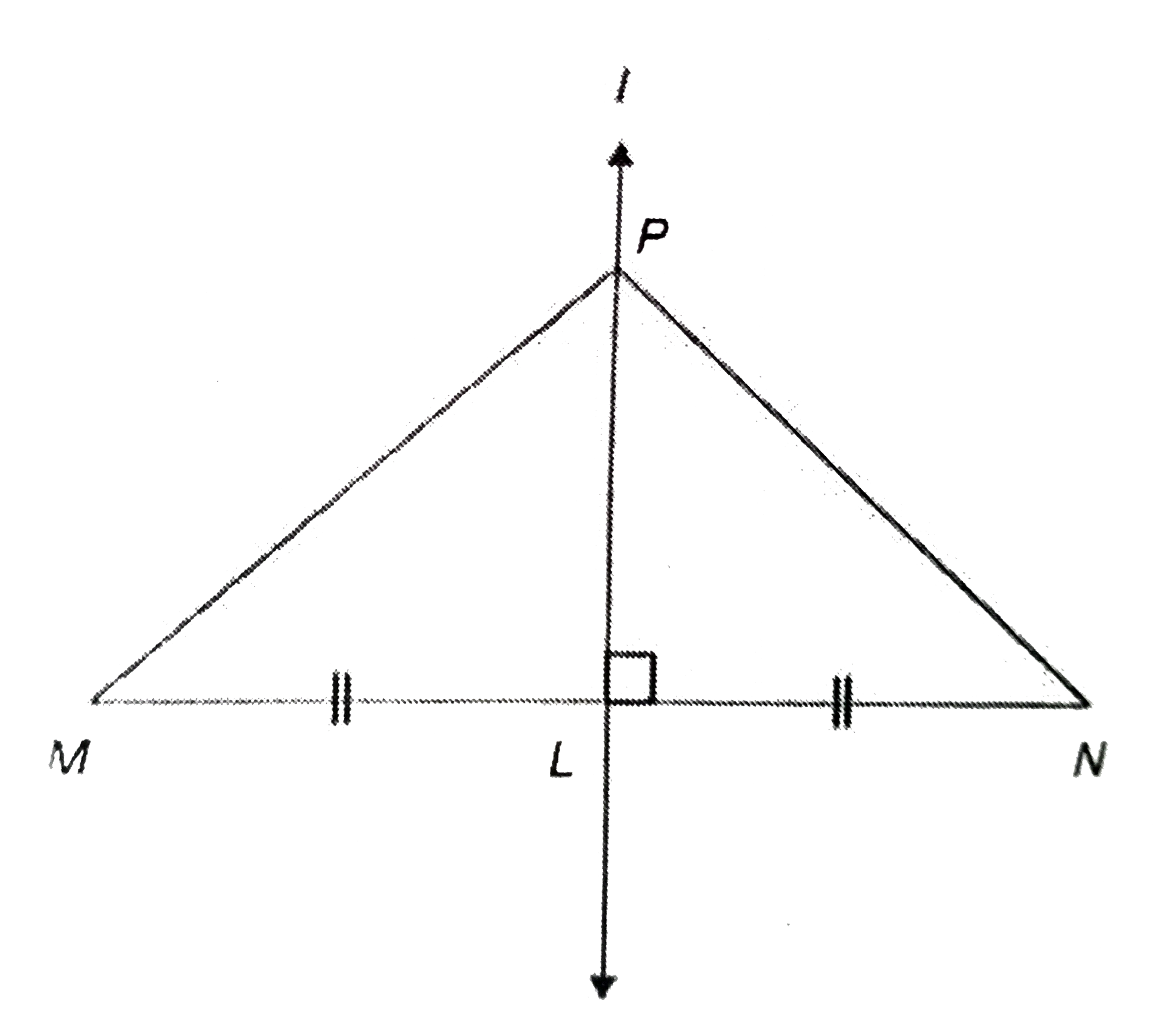
Given : M and N are two points on a plane. A is a point in the same plane such that AM = AN
To prove : A lies on the perpendicular bisector of MN.
Proof: Let L be the mid point of
If A coincides with L, then A lies on the bisector of MN.
Suppose A is different From L
Then, in and
ML = NL, AM = AN and AL is a common side.
By SSS congruence property,
( The corresponding elements of congruent triangles are equal)
But, ( Linear pair)
(from eq. (1))
So, Hence, is the perpendicular bisector of MN.
A lies on the perpendicular bisector of
Step : 2 Now, we prove that any point o the perpendiculat bisector of the line segment is equidistant from the end points of the line segments.
Given : MN is a line segment and P is point the perpendicualr bisector. L is the mid-point of MN
To prove : MP = NP.
Proof: If P coincides with L, then MP = NP .
Suppose P is different from L. Then, in and .
LP is the common side and
By the SAS congruence side and
So, MP = PN( The corresponding elements of congruent triangles are equal. )
Any point on the perpendicular bisector of is equidistant from point M and N.
Hence, from step I and step II of the proof, it can be said that the loucs of point equidistant from two fixed points is the perpendicualr bisector of the line segment joining the two points.

|
Topper's Solved these Questions
- LOCUSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LOCUSEXERCISE - Very short Answer Question
15 Videos
- LOCUSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LOCUSEXERCISE - Short Answer Question
8 Videos
- LINEAR EQUATIONS AND INEQUATIONSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONSEXERCISE - level 3
10 Videos
- LOGARITHMSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LOGARITHMSEXERCISE - Level 3 MCQ
15 Videos
Similar Questions
Knowledge Check
Statement-1: The locus of point z satisfying ∣∣∣3z+i2z+3+4i∣∣∣=32 is a straight line.
Statement-2 : The locus of a point equidistant from two fixed points is a straight line representing the perpendicular bisector of the segment joining the given points.AStatement-1 is True, Statement-2 is True: Statement-2 is a correct exp,anation for statement-1.BStatement-1 is true, statement -2 is true, Statement-2 is not a correct explanation for statement-1.CStatement-1 is True, statement-2 is false,Dstatement-1 is False, Statement-2 is true.Statement-1: If z is a complex number satisfying (z−1)n=zn , n∈N, then the locus of z is a straight line parallel to imaginary axis.
Statement-2: The locus of a point equidistant from two given points is the perpendicular bisector of the line segment joining them.AStatement-1 is True, Statement-2 is True: Statement-2 is a correct explanation for statement-1.BStatement-1 is true, statement -2 is true, Statement-2 is not a correct explanation for statement-1.CStatement-1 is True, statement-2 is false,Dstatement-1 is False, Statement-2 is true.Statement - 1 : If the perpendicular bisector of the line segment joining points A (a,3) and B( 1,4) has y-intercept -4 , then a=±4.
Statement- 2 : Locus of a point equidistant from two given points is the perpendicular bisector of the line joining the given points .AStatement -1 is True , Statement - 2 is true , Statement- 2 is a correct explanation for statement - 3BStatement-1 is True , Statement-2 is True , Statement -2 is not a correct explanation for Statement - 1 .CStatement-1 is True , Statement - 2 is False .DStatement - 1 is False , Statement -2 is True .
Interior point of a line segment
View SolutionThe locus of a point equidistant from two intersecting lines is
View SolutionTo construct the perpendicular bisector of a given line segment.
View SolutionDraw the perpendicular bisector of the line segment AB=5 cm.
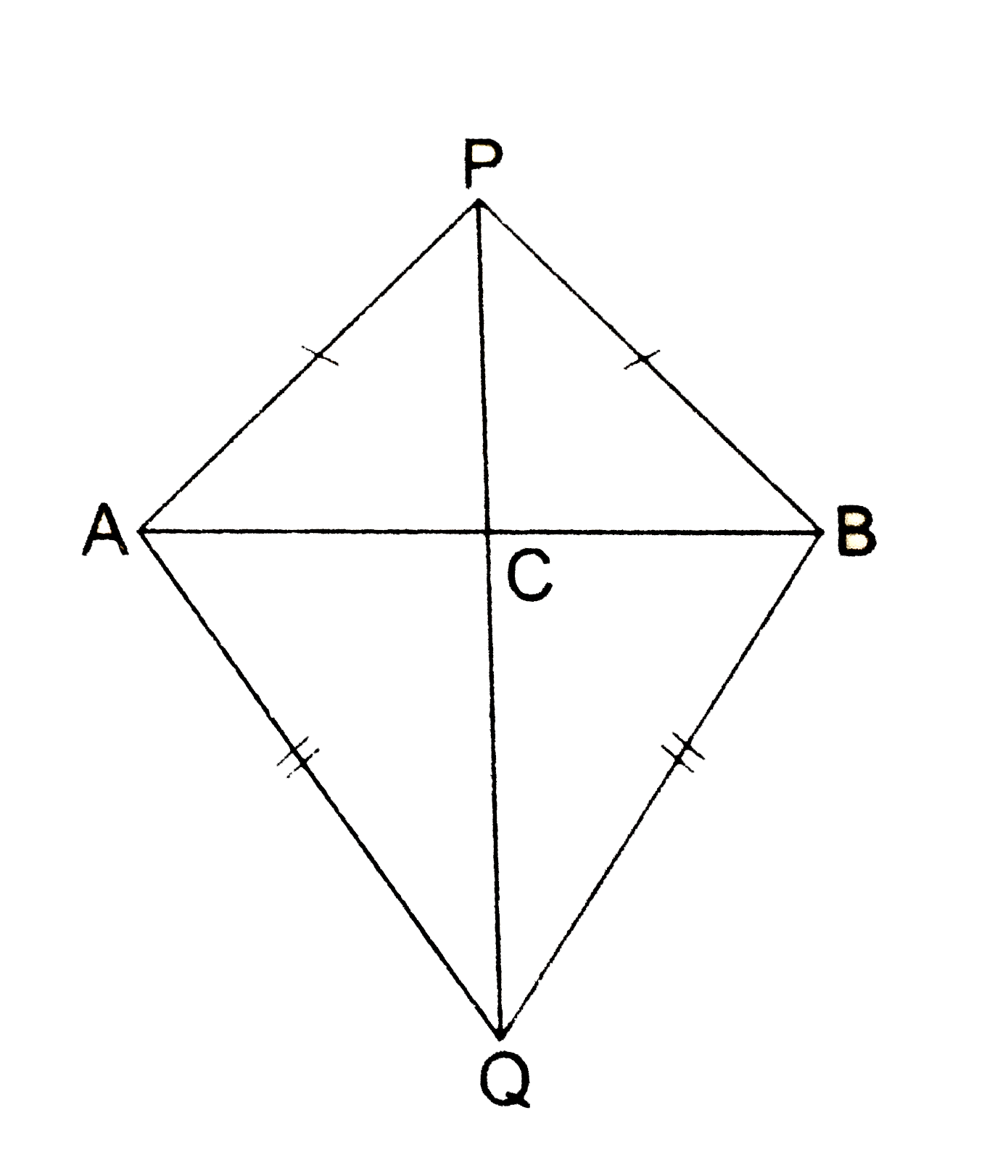
View SolutionIn the given figure, AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B. Show that the line PQ is the perpendicular bisector of AB.
View Solution
