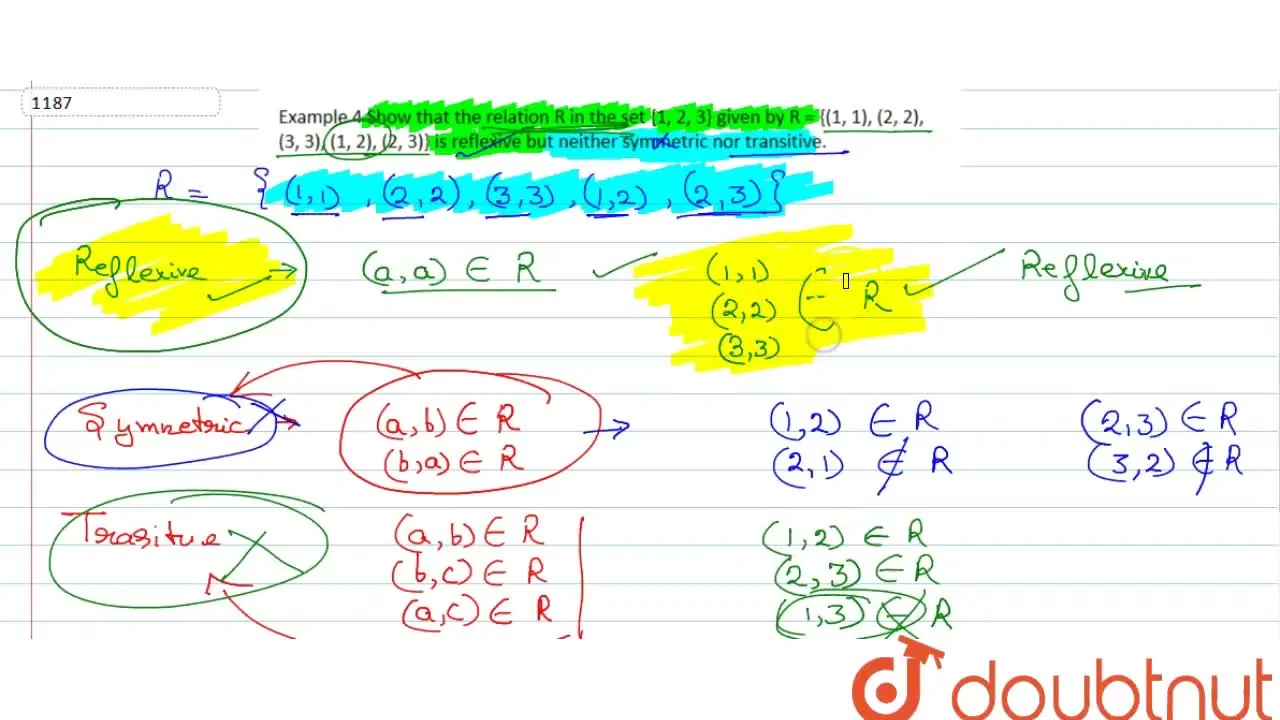
Show that the relation R in the set {1,2,3}given by R={(1,1),(2,2),(3,3),(1,2),(2,3)}is reflexive but neither symmetric nor transitive.
Here, A={1,2,3}
R={(1,1),(2,2),(3,3),(1,2),(2,3)}
As R contains (1,1),(2,2),(3,3), it is reflexive.
R contains (1,2),(2,3) but does not contain (2,1),(3,2), so it is not symmetric.
R contains (1,2),(2,3) but does not contain (1,3), so it is not transitive.
Similar Questions
Show that the relation R on the set A={1, 2, 3} given by R={(1, 1), (2, 2), (3, 3), (1, 2), (2,3 )} is reflexive but neither symmetric nor transitive.
View SolutionLet A={1,2,3}andR={(1,1),(2,2),(3,3),(1,2),(2,3)}.
show that R is reflexive but neither symmetric nor transitive .View SolutionThe relation in the set A = {1, 2, 3} given by R = {(2,3),(3,2),(1,1)} is:
View SolutionThe relation R on the set A = {1, 2, 3} defined as R ={(1, 1), (1, 2), (2, 1), (3, 3)} is reflexive, symmetric and transitive.
View SolutionShow that the relation R in the set {1, 2, 3} defined as:
(a) R={(1,2),(2,1)}
is symmetric, but neither reflexive nor transitive
(b) R={(1,1),(2,2),(3,3),(1,2),(2,3)}
is reflexive, but neither symmetric nor transitive
(c ) R={(1,3),(3,2),(1,2)}
is transitive, but neither reflexive nor symmetric.View SolutionIf R is a relation on the set A={1, 2, 3} given by R=(1, 1), (2, 2), (3, 3) , then R is (a) reflexive (b) symmetric (c) transitive (d) all the three options
View SolutionShow that the relation R in the set {1,2,3}given by R={(1,2),(2,1)}is symmetric but neither reflexive nor transitive.
View SolutionLetR be the relation on the seM = {1, 2, 3, 4} given by R = {(1,2), (2,2), (1,1), (4,4), (1,3), (3, 3), (3,2)}. Then
View SolutionShow that the relation R on the set A={1, 2, 3} given by R={(1, 2), (2, 1)} is symmetric but neither reflexive nor transitive.
View SolutionCheck whether the relation R={(1,1),(2,2)(3,3),(1,2),(2,3),(1,3)} is reflexive,symmetric and transitive or not.
View Solution