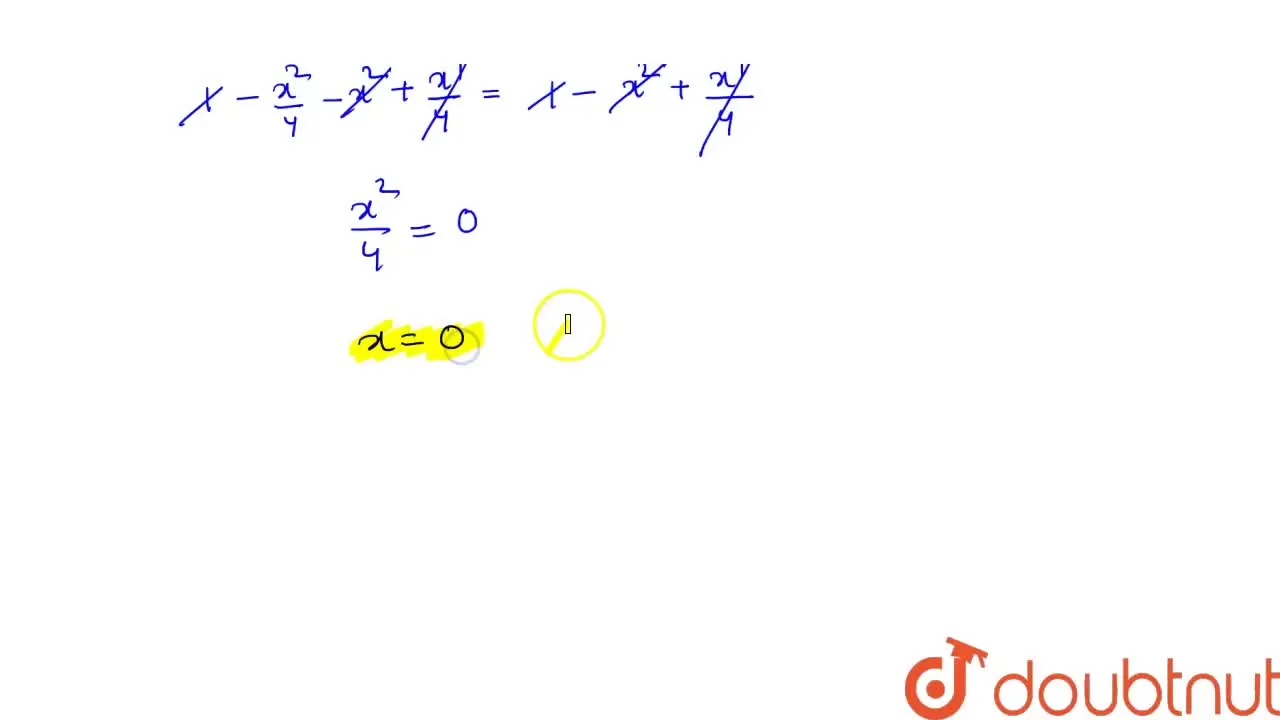
Solve :
Video Solution
Text Solution
for
L.H.S. , hence R.H.S.
Since is a decreasing function, we get
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.112videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.26videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - JEE Previous Year20videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 109videos
JEE 2019
Similar Questions
cos−1{12x2+√1+x2√1−x24}=cos−1(x2)−cos−1x
View SolutionProve that 2cos−1x=sin−1(2x√1−x2)
View Solutionf(x)=cos−1(x2√1+x2)
View SolutionSolve cos−1x>cos−1x2
View Solution2cos−1x=cos−1(2x2−1)
View Solutioncos−1(√1+x−√1−x2)
View Solutioncos−1(2√x1+x)
View Solutioncos−1(√1+cosx2)
View Solutioncos−1{x√x2+a2)
View SolutionSolve 2cos−1x=sin−1(2x√1−x2)
View Solution