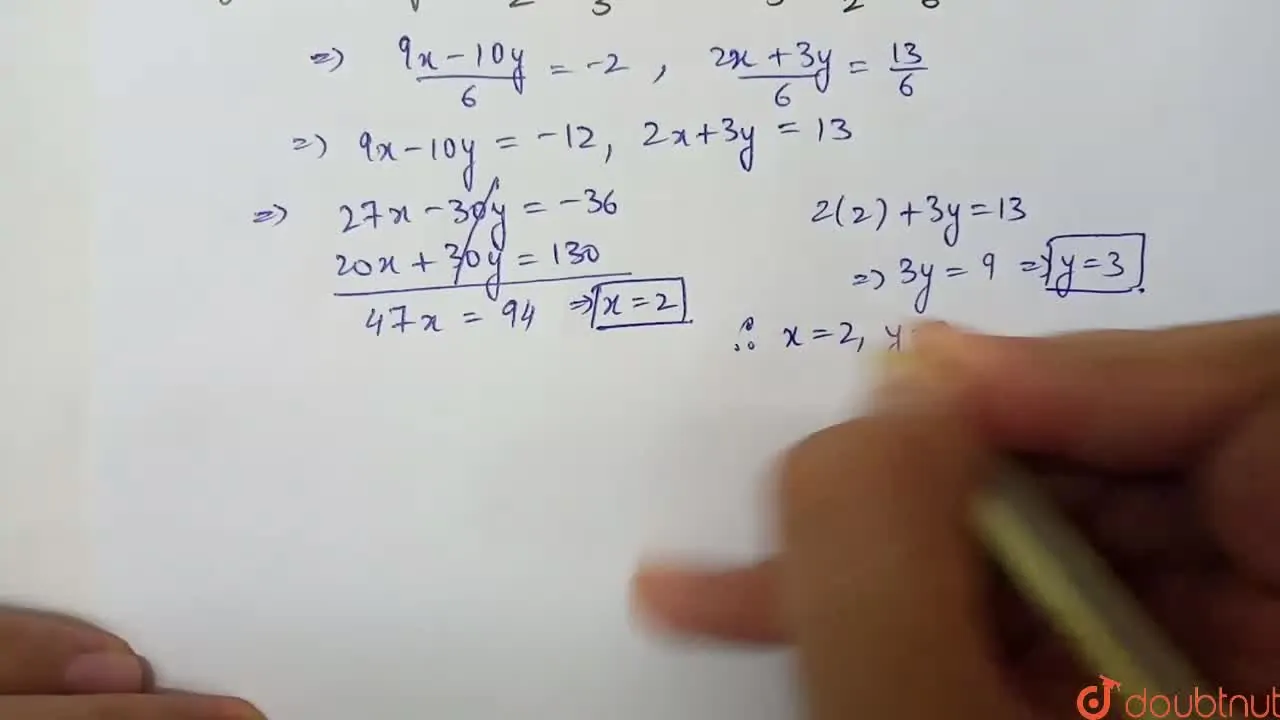Solve for xandy :
3x2−5y3=−2,x3+y2=136
(3,2)
(2,3)
(2,4)
(4,2)
The correct Answer is:B
The given system of equations may be written as
9x−10y+12=0 … (i)
2x+3y−13=0 … (ii)
From (ii) we get y=13−2x3
Substituting y=13−2x3 in (i), we get
9x−10(13−2x)3+12=0
⇒27x−10(13−2x)+36=0
⇒27x−130+20x+36=0
⇒47x−94=0⇒47x=94⇒x=9447=2.
Substituting x=2in (i), we get
9×2−10y+12=0⇒10y=30⇒y=3010=3.
Hence, x=2andy=3 is the required solution.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Exercise 3A29videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Exercise 3B50videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Multiple Choice Questions (Mcq)25videos
HEIGHTS AND DISTANCES
- BOOK - RS AGGARWALCHAPTER - MEAN,MEDAN,MODE OF GROUPED,DATA CUMULATIVE FREQUENCY GRAPH AND OGIVE EXERCISE - Test Yourself18videos
MEAN,MEDAN,MODE OF GROUPED,DATA CUMULATIVE FREQUENCY GRAPH AND OGIVE
Similar Questions
(2) 3x2−5y3=−2;x3+y2=136
View SolutionSolve for xandy :
2x+3y=13,5x−4y=−2(x≠0andy≠0)View SolutionSolve for x and y :
2x + 3y = 46,
3x + 5y = 74View SolutionSolve the following pair of linear equations by the substitution method:
3x2−5y3=−2
x3+y2=136View SolutionSolve for x and y:
2x - 3y-13 =0 , 3x -2y+12 =0View SolutionSolve the pair of linear equations :
3x2−5y3=−2andx3+y3=136.View SolutionSolve the following equations :
x2+2y3=−1
x3−y2=136.View SolutionSolve for x and y:
x−y=3andx+2y=6.View SolutionSolve the following pair of linear equations by the substitution method:
3x2−5y3=−2
x3+y2=136View SolutionSolve the pair of linear equation by substitution method.
3x2−5y3=−2,x2+y2=136View Solution