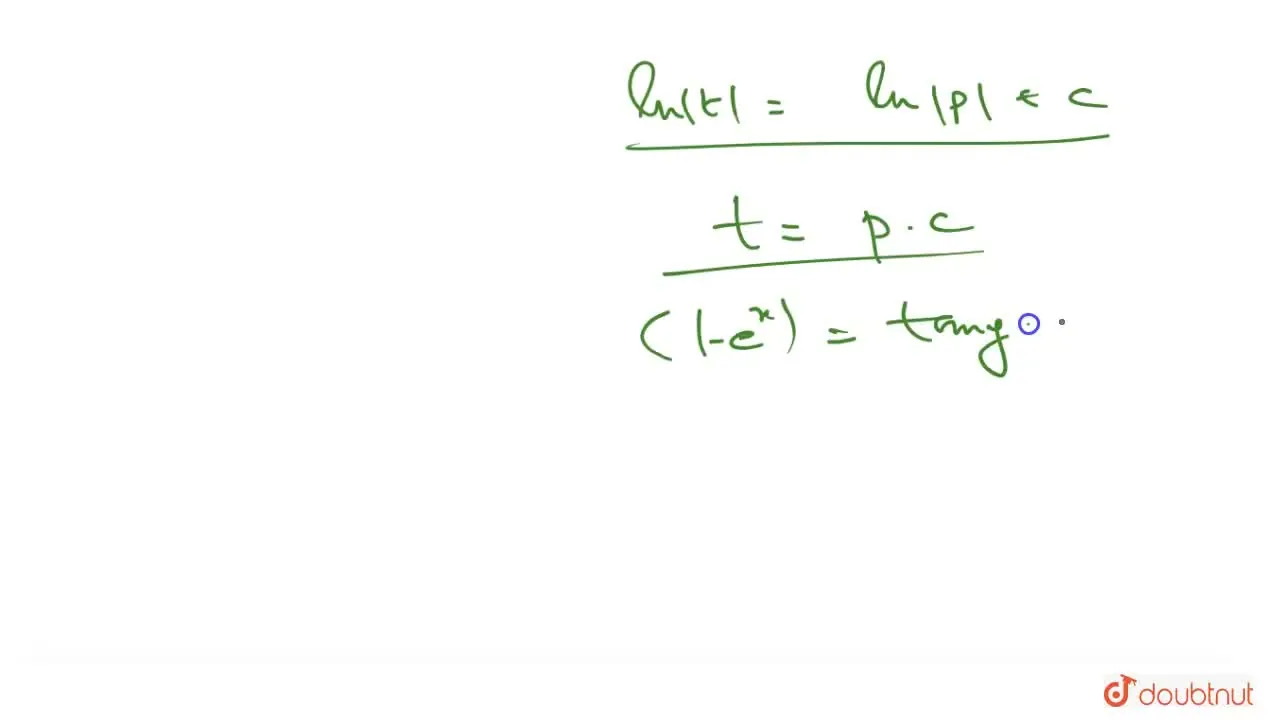Solve the differential equation extanydx+(1−ex)sec2ydy=0
Integrating the equation, we get
∫ex1−exdx+∫sec2ytanydy=0
Put 1−ex=t for 1st integral and tan y = u for 2nd integral
⇒−exdx=dt and sec2ydy=du
⇒∫−dtt+∫duu=0
⇒−In|t|+In|u|=InC
⇒u=Ct
⇒tany=C(1−ex)
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Try Yourself26videos
DIFFERENTIAL EQUATIONS
- BOOK - AAKASH INSTITUTECHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Assignment (Section - A) Competition Level Questions35videos
DIFFERENTIAL EQUATIONS
- BOOK - AAKASH INSTITUTECHAPTER - DETERMINANTS EXERCISE - SECTION - J12videos
DETERMINANTS
- BOOK - AAKASH INSTITUTECHAPTER - INTEGRALSEXERCISE - Try yourself50videos
INTEGRALS
Similar Questions
What is the solution of the differential equation 3extanydx+(1+ex)sec2ydy=0 ?
View SolutionWhat is the solution of the differential equation 3extanydx+(1+ex)sec2ydy=0 ?
View Solutionwhat is the solution of the differential equaiton
3extanydx+(1+ex)sec2ydy=0 ?View SolutionFind the particular solution of the differential equation 3extanydx+(1+ex)sec2ydy=0, when x= 0, y=π
View SolutionFind the general solution of each of the following differential equations:
extanydx+(1−ex)sec2ydy=0View SolutionSolve the following differential equation: extany dx+(1−ex)sec2y dy=0
View SolutionSolve the differential equation :
sec2xtanydx+sec2ytanxdy=0View SolutionSolve the following differential equations
3extanydx+(1−ex)sec2ydy=0 given that y=π4, when x=1.View SolutionFind the general solution of each of the following differential equations:
3extanydx+(1−ex)sec2ydy=0View SolutionSolve the following differential equation.
(1)extan2ydx+(ex−1)sec2ydy=0View Solution