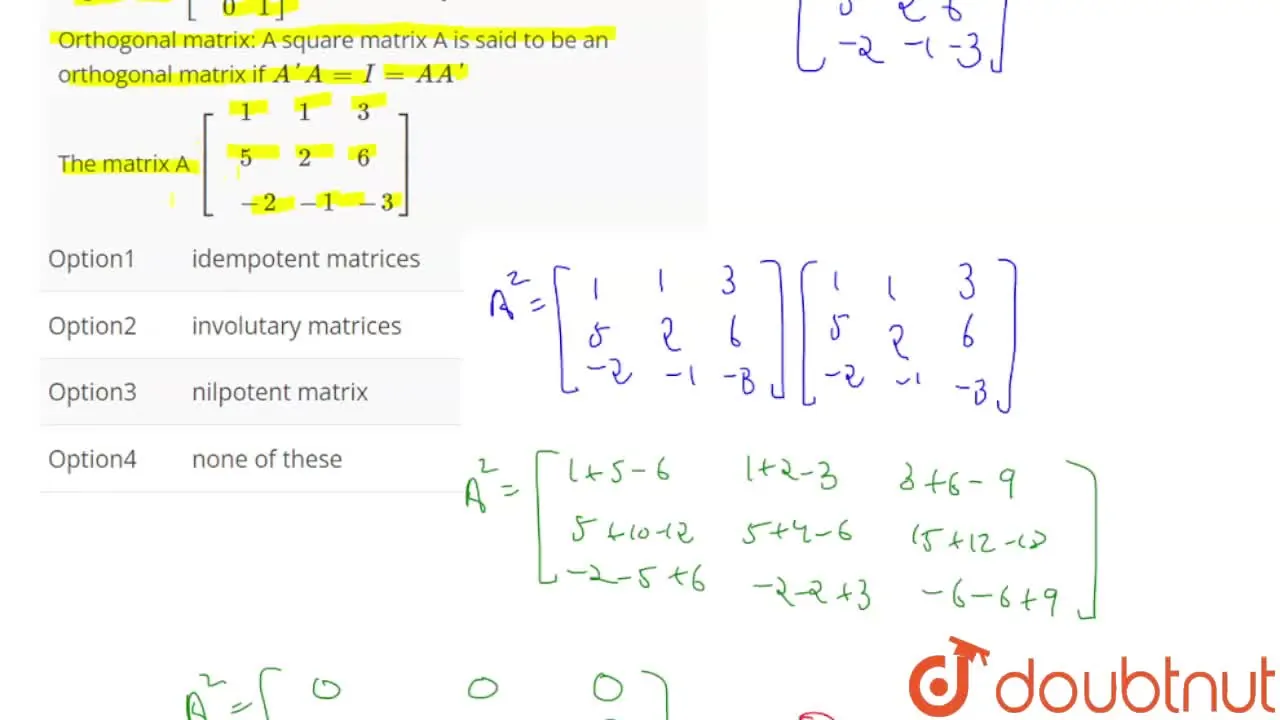
Some special square matrices are defined as follows. Nilpotent matrix: A square matrix. A is said to be nilpotent (of order 2)if, A2=O. A square matrix is said to be nilpotent of order p, if p is the least positive integer such that Ap=O.
Idempotent matrix: A square matrix A is said to be idempotent if, A2=A.
e.g.[1001] is an idempotent matrix.
Involutory matrix: A square A is said to be involutary if A2=I, Ibeing the identity matrix.
e.g..A=[1001] is an involutary matrix.
Orthogonal matrix: A square matrix A is said to be an orthogonal matrix if A'A=I=AA'
The matrix A ⎡⎢⎣113526−2−1−3⎤⎥⎦
idempotent matrices
involutary matrices
nilpotent matrix
none of these
The correct Answer is:C
Step by step video, text & image solution for Some special square matrices are defined as follows. Nilpotent matrix: A square matrix. A is said to be nilpotent (of order 2)if, A^(2)=O. A square matrix is said to be nilpotent of order p, if p is the least positive integer such that A^(p)=O. Idempotent matrix: A square matrix A is said to be idempotent if, A^(2)=A. e.g.[{:(,1,0),(,0,1):}] is an idempotent matrix. Involutory matrix: A square A is said to be involutary if A^(2)=I, I being the identity matrix. e.g..A=[{:(,1,0),(,0,1):}] is an involutary matrix. Orthogonal matrix: A square matrix A is said to be an orthogonal matrix if A' A=I=A A' The matrix A [{:(,1,1,3),(,5,2,6),(,-2,-1,-3):}] by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - RESONANCECHAPTER - MATRICES & DETERMINANTEXERCISE - EXERCISE-331videos
MATRICES & DETERMINANT
- BOOK - RESONANCECHAPTER - MATRICES & DETERMINANTEXERCISE - PART-II:28videos
MATRICES & DETERMINANT
- BOOK - RESONANCECHAPTER - MATRICES & DETERMINANTEXERCISE - EXERCISE-220videos
MATRICES & DETERMINANT
- BOOK - RESONANCECHAPTER - INDEFINITE INTEGRATION EXERCISE - SELF PRACTIC PROBLEMS25videos
INDEFINITE INTEGRATION
- BOOK - RESONANCECHAPTER - NUMBER THEORYEXERCISE - Exercise -2 (PART - II)4videos
NUMBER THEORY
Similar Questions
Some special square matrices are defined as follows. Nilpotent matrix: A square matrix. A is said to be nilpotent (of order 2)if, A2=O. A square matrix is said to be nilpotent of order p, if p is the least positive integer such that Ap=O.
Idempotent matrix: A square matrix A is said to be idempotent if, A2=A.
e.g.[1001] is an idempotent matrix.
Involutory matrix: A square A is said to be involutary if A2=I, Ibeing the identity matrix.
e.g..A=[1001] is an involutary matrix.
Orthogonal matrix: A square matrix A is said to be an orthogonal matrix if A'A=I=AA'
The matrix A ⎡⎢⎣113526−2−1−3⎤⎥⎦View SolutionNilpotent Matrix
View SolutionIdempotent Matrix
View SolutionSome special square matrices are defined as follows. Nilpotent matrix: A square matrix. A is said to be nilpotent (of order 2)if, A2=O. A square matrix is said to be nilpotent of order p, if p is the least positive integer such that Ap=O.
Idempotent matrix: A square matrix A is said to be idempotent if, A2=A.
e.g.[1001] is an idempotent matrix.
Involutory matrix: A square A is said to be involutary if A2=I, Ibeing the identity matrix.
e.g..A=[1001] is an involutary matrix.
Orthogonal matrix: A square matrix A is said to be an orthogonal matrix if A'A=I=AA'
If ⎡⎢⎣02βγαβ−γα−βγ⎤⎥⎦ is orthogonal, thenView SolutionSome special square matrices are defined as follows. Nilpotent matrix: A square matrix. A is said to be nilpotent (of order 2)if, A2=O. A square matrix is said to be nilpotent of order p, if p is the least positive integer such that Ap=O.
Idempotent matrix: A square matrix A is said to be idempotent if, A2=A.
e.g.[1001] is an idempotent matrix.
Involutory matrix: A square A is said to be involutary if A2=I, Ibeing the identity matrix.
e.g..A=[1001] is an involutary matrix.
Orthogonal matrix: A square matrix A is said to be an orthogonal matrix if A'A=I=AA'
If A and B are two square matrices such that AB=A & BA=B then A&B areView SolutionA square matrix A is said to be symmetric matrix if
View SolutionA square matrix A is said to be symmetric matrix if
View SolutionWhen a square matrix is said to be invertible
View SolutionA square matrix A is said skew - symmetric matrix if
View SolutionInverse OF square matrix || Orthogonal matrix
View Solution