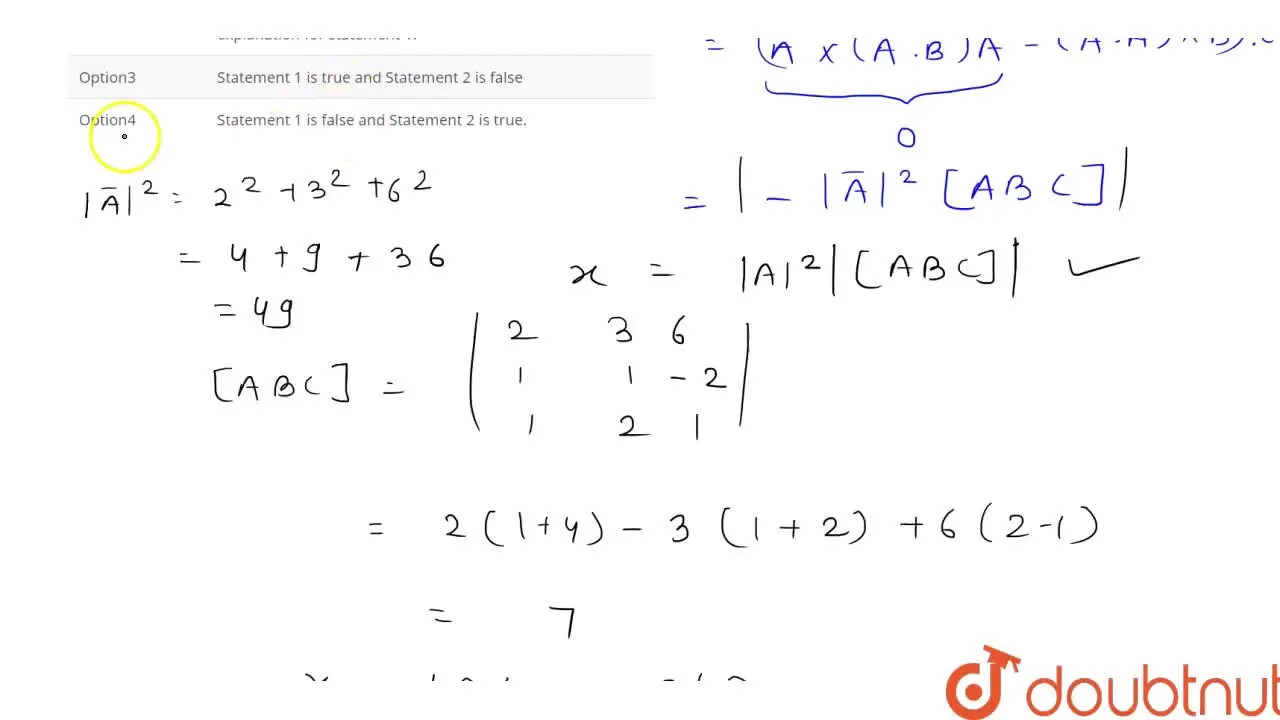
Statement 1: →A=2ˆi+3ˆj+6ˆk,→B=ˆi+ˆj−2ˆkand→C=ˆi+2ˆj+ˆk then ∣∣→A×(→A×(→A×→B)).→C∣∣=243 Statement 2: ∣∣→A×(→A×(→A×→B)).→C∣∣=∣∣→A∣∣2∣∣[→A→B→C]∣∣
Both the statements are true and statement 2 is the correct explanation for statement 1.
Both statements are true but statement 2 is not the correct explanation for statement 1.
Statement 1 is true and Statement 2 is false
Statement 1 is false and Statement 2 is true.
The correct Answer is:d
→A×(→A.→B)→A−(→A.→A)→B).→C
⎛⎜
⎜⎝=→A×(→A.→B)→Azero−(→A.→A)×→B⎞⎟
⎟⎠.→C
=−∣∣→A∣∣2[→A→B→C]
now ∣∣→A∣∣2=4+9+36=49
[→A→B→C]=∣∣
∣∣23611−2121∣∣
∣∣
2( 1+4) -1 (3 -12) +1 (-6-6)
= 10 +9 -12 =7
∣∣→A∣∣2[→A→B→C]∣=49×7=343
Related Playlists
- BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - JEE Previous Year (Single Question)28videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - JEE Previous Year (Multiple Question)11videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise 2.318videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises1316videos
CONIC SECTIONS
- BOOK - CENGAGECHAPTER - LIMITS AND DERIVATIVESEXERCISE - Solved Examples And Exercises320videos
LIMITS AND DERIVATIVES
Similar Questions
If →a=2ˆi+3ˆj+ˆk,→b=ˆi−2ˆj+ˆk and →c=−3ˆi+ˆj+2ˆk, then [→a→b→c]=
View SolutionIf →a=7ˆi+3ˆj−5ˆk,→b=2ˆi+5ˆj−ˆkand→c−ˆi+2ˆj+4ˆk, then verify that →a×(b+c)=→a×→b+→a×→c
View SolutionIf →a=7ˆi+3ˆj−6ˆk, →b=2ˆi+5ˆj−ˆk and →c=−ˆi+2ˆj+4ˆk. Find (→a−→b)×(→c−→b).
View SolutionIf →A=2ˆi+ˆj−3ˆk,→B=ˆi−2ˆj+ˆk and →C=−ˆi+ˆj−4ˆk, Calculate (i) →A.(→B×→C),(ii)→C(→A×→B),(iii)→A×(→B×→C)
View SolutionIf →A2ˆi+ˆj−ˆk,→B=ˆi+2ˆj+3ˆk,→C=6ˆi−2ˆj−6ˆk angle between (→A+→B)and→C will be
View SolutionIf →a=ˆi+ˆj+ˆk,→b=2ˆi+ˆj−ˆkand→c=4ˆi+3ˆj+ˆk then value of ((→a+→b)×(→a−(→a−→b)×→b)))×→c is
View SolutionIf →a=2ˆi−3ˆj,→b=ˆi+ˆj−ˆk,→c=3ˆi−ˆk, find [a→b→c]
View SolutionIf →A=2ˆi+ˆj−ˆk.→B=ˆi+2ˆj+3ˆkand→C=6ˆi−2ˆj−6ˆk then the angle between (→A+→B)and→C will be :-
View SolutionGiven the vector →A=2ˆi+3ˆj−ˆk,→B=3ˆi−2ˆj−2ˆk&→C=pˆi+pˆj+pˆk. Find the angle between (→A−→B)&→C
View SolutionIf →a=2ˆi+2ˆj−ˆk,→b=3ˆi−ˆj−ˆkand→c=ˆi+2ˆj−3ˆk then verify that →a×(→b×→c)=(→a.→c)→b−(→a.→b)→c.
View Solution