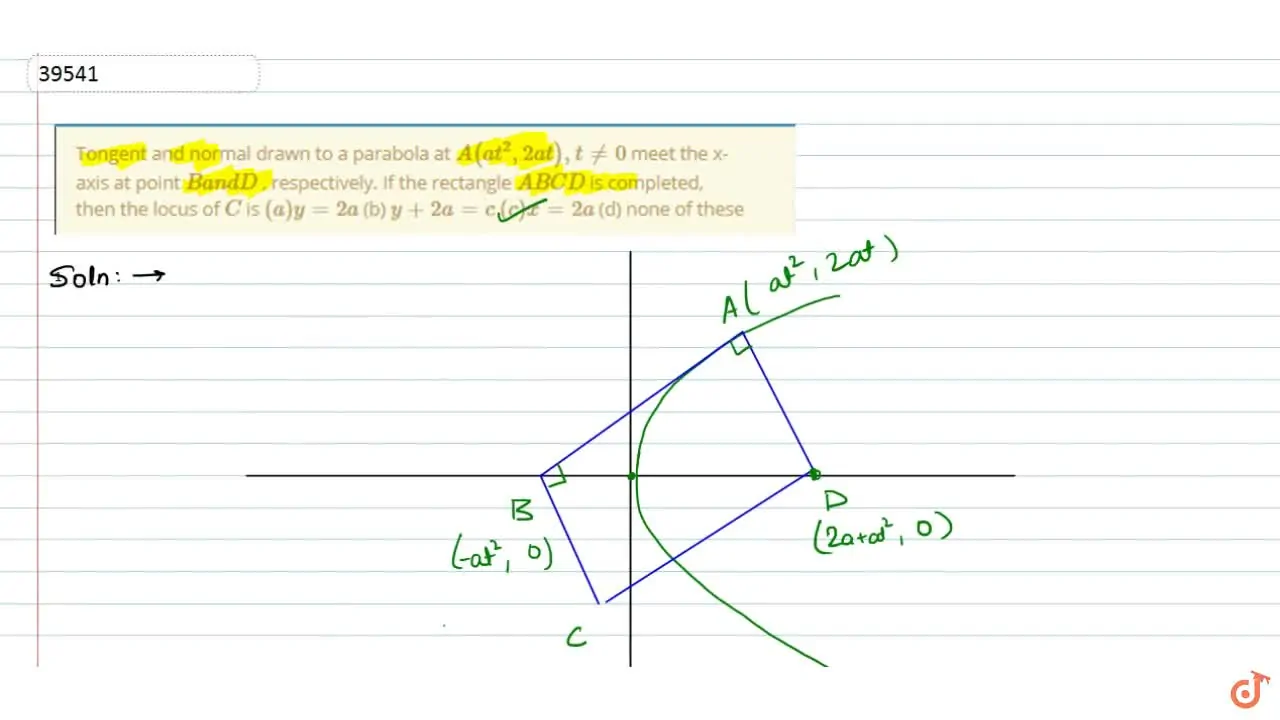
Tongent and normal drawn to a parabola at A(at2,2at),t≠0 meet the x-axis at point BandD , respectively. If the rectangle ABCD is completed, then the locus of C is y=2a (b) y+2a=c x=2a (d) none of these
y=2a
x=2a−y24a
x=2a
none of these
The correct Answer is:B
(2) The equation of tangent and normal at A are yt=x+at2andy=−tx+2at+at3, respectively.
Therefore, B≡(−at2,0)andD≡(2a+at2,0). If ABCD is a rectangle, then the midpoint of BD and AC will be coincident. So,
h+at2=2a+at2−at2,
k+2at=0
orh=2a−at2,t=−k2a
Therefore, the locus is
x=2a−y24a

Related Playlists
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Multiple)26videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Comprehension)41videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise 5.79videos
PARABOLA
- BOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Question Bank19videos
PERMUTATION AND COMBINATION
Similar Questions
Tongent and normal drawn to a parabola at A(at2,2at),t≠0 meet the x-axis at point BandD , respectively. If the rectangle ABCD is completed, then the locus of C is (a)y=2a (b) y+2a=c (c)x=2a (d) none of these
View SolutionA straight line is drawn through P(3,4) to meet the axis of x and y at AandB , respectively. If the rectangle OACB is completed, then find the locus of C.
View SolutionTangents and normal drawn to the parabola y2=4ax at point P(at2,2at),t≠0, meet the x-axis at point TandN, respectively. If S is the focus of theparabola, then SP=ST≠SN (b) SP≠ST=SN SP=ST=SN (d) SP≠ST≠SN
View SolutionIf a tangent to the parabola y2=4ax meets the x-axis at T and intersects the tangents at vertex A at P, and rectangle TAPQ is completed, then find the locus of point Q.
View SolutionIf a tangent to the parabola y2=4ax meets the axis of the parabola in T and the tangent at the vertex A in Y, and the rectangle TAYG is completed, show that the locus of G is y2+ax=0.
View SolutionIf a tangent to the parabola y2=4ax meets the axis of the parabola in T and the tangent at the vertex A in Y, and the rectangle TAYG is completed, show that the locus of G is Y2+ax=0.
View SolutionThe tangent PT and the normal PN to the parabola y2=4ax at a point P on it meet its axis at points T and N, respectively. The locus of the centroid of the triangle PTN is a parabola whose:
View SolutionTangent and normal at any point P of the parabola y2=4ax(a>0) meet the x-axis at T and N respectively. If the lengths of sub-tangent and sub-normal at this point are equal, then the area of ΔPTN is given by
View SolutionIf the tangent drawn to the hyperbola x2a2−y2b2=1 at any point P meets the coordinate axes at the points A and B respectively. If the rectangle OACB (O being the origin) is completed, where C lies on x2a2−y2b2=λ . Then, the value of λ is:
View SolutionIf the normal at(1, 2) on the parabola y2=4x meets the parabola again at the point (t2,2t) then the value of t, is
View Solution