Tangent are drawn from the point p(3,4) to the ellipse x29+y24=1 tochinhg the ellipse at point A and B .
the coordinates of a and B are Solution in Tamil
(3,0)and(0,2)
(−8/5,2√161/15)and(−9/5,8/5)
(8/5,2√161/15and(0,2)
(3,0)and(−9/5,8/5)
Given ellipse x29+y24=1
The equation of tangent having slope m is 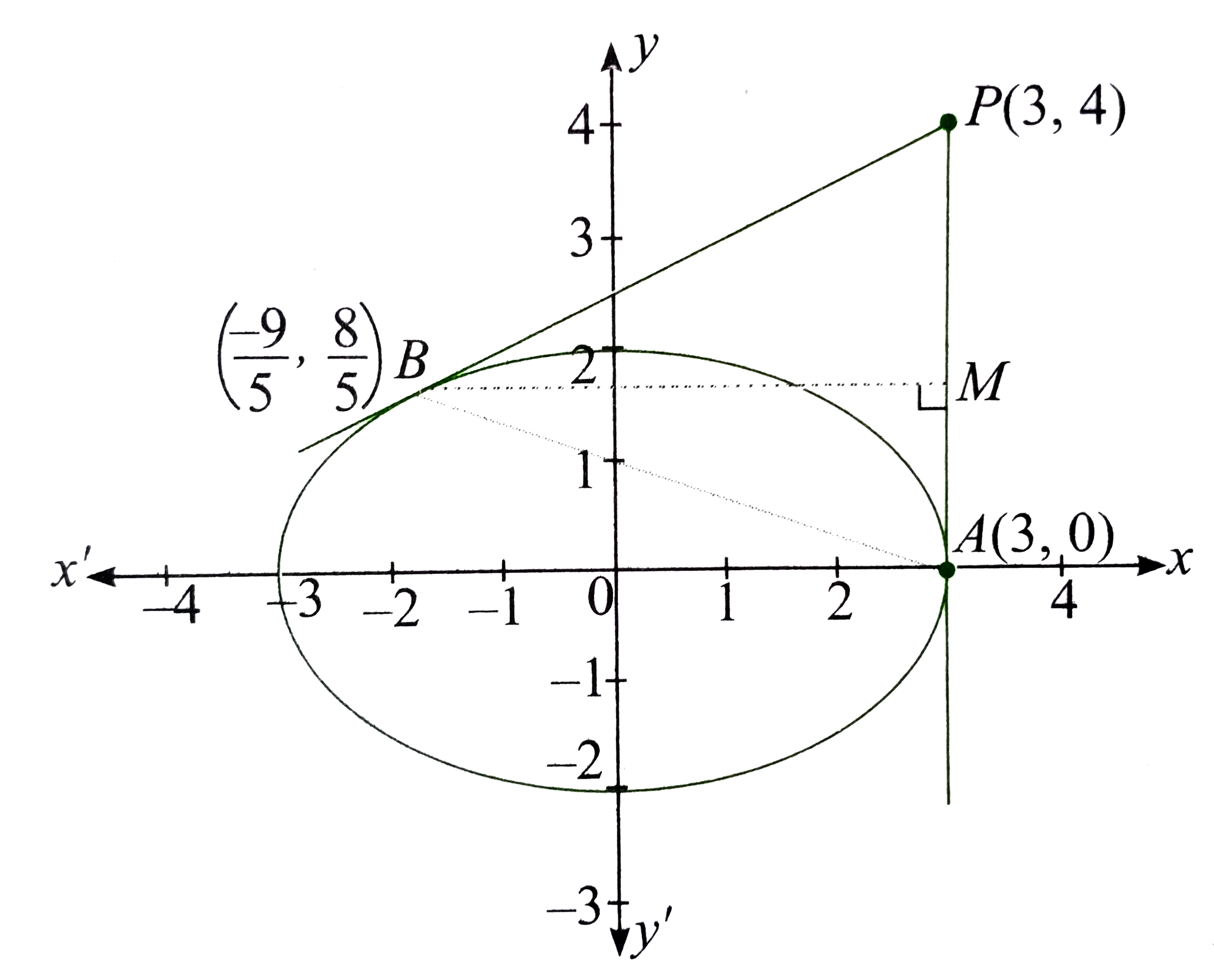
y=mx+√9m2+4
Sqaring , we have
16+9m2−24m=9m2+4
or m=1224=12
Threrefpre, the equation of tangent is y−4=−(x−3)prx−2y+5=0 (1)
Let the point of contact on the curve be B(α,β)
Equation of tangent at this point is xα9+yβ4−1=0 (2)
Comparing equations (1) and (2)
α/91=β/4−2=−15
or α=−95,β=85 ∴B≡(−95,85)
Another slope of tangent is ∞ then the equation of tanents is x=3 and the coresponding point of cocntact is A(3,0)
Similar Questions
बिंदु P(3,4) से दीर्घवृत x29+y24=1 पर स्पर्शियां डाली जाती हैं जो दीर्घवृत को बिंदुओं A एवं B पर स्पर्श करती हैं|
A तथा B के निर्देशांक निम्न हैं
View SolutionTangents are drawn through the point (4,√3) to the ellipse x216+y29=1. The points at which these tangents touch the ellipse are
View Solutionबिन्दु P(3, 4) से दीर्घवृत्त x29+y24=1 पर खींची गई स्पर्श रेखाएं इस दीर्घवृत्त को A एवं B बिन्दुओं पर स्पर्श करती है। A तथा B के निर्देशांक हैं : (i) (3,0) एवं (0,2) (ii) (−85,2√16115) एवं (−95,85) (iii) (−85,2√16115) एवं (0,2) (iv) (3,0) एवं (−95,85)
View Solutionबिन्दु P(3, 4) से दीर्घवृत्त x29+y24=1 पर खींची गई स्पर्श रेखाएं इस दीर्घवृत्त को A एवं B बिन्दुओं पर स्पर्श करती है।
त्रिभुज PAB का लम्बकेन्द्र है ।
View SolutionTangents are drawn from the point P(3,4) to the ellipse x^(2)/9+y^(2)/4=1 touching the ellipse at point A and B. Q. The coordinates of A and B are
View SolutionTangents are drawn from the point P(3,4) to the ellipse x29+y24=1 touching the ellipse at point A and B. Q. The orthocenter of the trianlge PAB is
View SolutionTangents are drawn from the point P(3,4) to the ellipse x^(2)/9+y^(2)/4=1 touching the ellipse at point A and B. Q. The equation of the locus of the points whose distance from the point P and the line AB are equal, is
View SolutionTangents are drawn from the point P(3, 4) to the ellipse x^2/9+y^2/4=1 touching the ellipse at points A and B.
View Solution
