The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
To find the angle measures x, y, and z in the parallelogram HOPE, we will follow these steps:
1. Identify the Given Angles:
- We know that one angle (let's call it angle H) is 70∘.
2. Find Angle 1:
- Since angle H and angle 1 are on the same straight line, they form a linear pair.
- Therefore, we can write the equation:
Angle 1+70∘=180∘
- Solving for angle 1:
Angle 1=180∘−70∘=110∘
3. Determine Angle X:
- In a parallelogram, opposite angles are equal.
- Therefore, angle x (which is opposite to angle 1) is:
x=Angle 1=110∘
4. Find Angle Y:
- Since EP is parallel to HO and HP acts as a transversal, we can use the property of vertically opposite angles.
- Thus, angle y is equal to angle 40 degrees (which is vertically opposite to angle Y):
y=40∘
5. Determine Angle Z:
- We know that angle H is 70∘ and angle E (which is adjacent to angle Z) is 40∘.
- Since EH is parallel to OP, we can use the property of corresponding angles:
Angle H=Angle E+z
- Therefore, we can write:
70∘=40∘+z
- Solving for z:
z=70∘−40∘=30∘
Final Angle Measures:
- x=110∘
- y=40∘
- z=30∘
Properties Used:
1. Linear Pair: The sum of angles on a straight line is 180∘.
2. Opposite Angles of a Parallelogram: Opposite angles are equal.
3. Vertically Opposite Angles: Angles opposite each other when two lines cross are equal.
4. Corresponding Angles: When a transversal crosses parallel lines, corresponding angles are equal.
- We know that one angle (let's call it angle H) is 70∘.
- Since angle H and angle 1 are on the same straight line, they form a linear pair.
- Therefore, we can write the equation:
Angle 1+70∘=180∘
- Solving for angle 1:
Angle 1=180∘−70∘=110∘
- In a parallelogram, opposite angles are equal.
- Therefore, angle x (which is opposite to angle 1) is:
x=Angle 1=110∘
- Since EP is parallel to HO and HP acts as a transversal, we can use the property of vertically opposite angles.
- Thus, angle y is equal to angle 40 degrees (which is vertically opposite to angle Y):
y=40∘
- We know that angle H is 70∘ and angle E (which is adjacent to angle Z) is 40∘.
- Since EH is parallel to OP, we can use the property of corresponding angles:
Angle H=Angle E+z
- Therefore, we can write:
70∘=40∘+z
- Solving for z:
z=70∘−40∘=30∘
- x=110∘
- y=40∘
- z=30∘
1. Linear Pair: The sum of angles on a straight line is 180∘.
2. Opposite Angles of a Parallelogram: Opposite angles are equal.
3. Vertically Opposite Angles: Angles opposite each other when two lines cross are equal.
4. Corresponding Angles: When a transversal crosses parallel lines, corresponding angles are equal.
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALSBOOK - NCERT ENGLISHCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.2
6 Videos
- SQUARES AND SQUARE ROOTSBOOK - NCERT ENGLISHCHAPTER - SQUARES AND SQUARE ROOTSEXERCISE - EXERCISE 6.4
9 Videos
- VISUALISING SOLID SHAPESBOOK - NCERT ENGLISHCHAPTER - VISUALISING SOLID SHAPESEXERCISE - EXERCISE 10.3
8 Videos
Similar Questions
In the adjacent figure HOPE is a parallelogram. Find the angle measures x, y and Z. State the geometrical truths you use to find them. (Figure)
View SolutionIn the given figure, ABCD is a parallelogram. Find the values of x, y and z
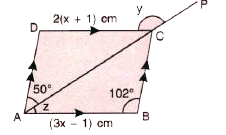
View SolutionIn Fig 3.26, BEST is a parallelogram. Find the values x, y and z.
View SolutionIn Figure, BEST is a parallelogram. Find the values of x, y and z.
View SolutionTwo adjacent angles of a parallelogram are as 2:3. Find the measures of all the angles.
View SolutionFind the angle measure x in the following figures.
View SolutionIn Figure, RICE is parallelogram. Find x, y, z.
View SolutionIn the given figure, find x,y and z.
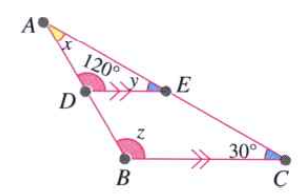
View SolutionFind the values of x,y and z in the given figure.

View SolutionIn the adjacent figure, find x+y+z
View Solution
